D-module Basics I

Its a bit embarassing for me, but I am only now really getting around to learning the theory of D-modules. Given that my research area is Noncommutative Geometry, Homological Algebra or maybe Representation Theory depending on when you ask me, this just shouldn’t be. I made slow progress through Bernstein’s notes last week, and then I found Schneiders’ notes a few days ago. They make a good compliment to Bernstein’s notes; where Bernstein is good about mentioning the underlying ways you should think about various tools, Schneiders is good about saying things clearly and writing out proofs. I tend to prefer the former kind of paper, until the moment I get lost and the lack of nitty-gritty to pour over trips me up.

Anywho, I am fond of explaining things as a method of solidifying thoughts in my head and turning vague concepts into concrete statements (one motivation for having the blog). It feels a little silly talking about something that I have already linked to better resources for, but I have never let that stop me in the past. Besides, Matt requested it, and I think it would be good to foster a bit of discussion, since one key factor in understanding why D-modules are cool is understanding how they connect to far-flung reaches of math. For more D-module stuff, especially a lengthy list of why mathematicians care about them, see the Secret Blogging Seminar’s pair of posts on the subject, especially the comments on the first post.

Today, I will define D-modules, and show how certain D-modules can describe solutions to various homogenous and inhomogenous partial differential equations.

Let $D_{\mathbb{C}^n}$ be the ring of regular differential operators on $\mathbb{C}^n$ . This is the ring of operators generated by

(1) multiplication by a polynomial on $\mathbb{C}^n$ , and

(2) partial differentiation with respect to one of the coordinate variables.

In this specific case, this ring is sometimes called the n-th Weyl algebra.

Notice that I have not specified which space of functions I am thinking of $D_{\mathbb{C}^n}$ acting on. A space with a prescribed action of $D_{\mathbb{C}^n}$ is called a (left) D-module. These could be polynomials, sections of a holomorphic vector bundle with flat connection, compactly supported smooth functions, or whatever.

Suppose that I fix such a space of functions $S$ , and further suppose that there is a homogenous partial differential equation of interest in this space. A PDE in $S$ looks like a series of $b$ equations of the form

$\sum_i P_{ji}u_i=0,\; 0\leq i \leq a,\; 0\leq j \leq b$

for fixed $P_{ji}\in D_{\mathbb{C}^n}$ and indeterminant $u_i\in S$ . The goal is then to find out which $\{u_i\} \in S^a$ satisfy these equations. Denote the space of such solutions as $S^P$ .

What do we know about a solution $\{u_i\}\in S^P$ ? Well, I can talk about $\sum_i Q_i(u_i)$ , a linear combination of differential operators acting on the functions in my solution. However, in general I know nothing about this linear combination, unless I happen to satisfy one of the defining equations, which must vanish. Categorically, I have described a morphism of D-modules,

$D_{\mathbb{C}^n}^a\rightarrow S$ ,

which sends $\oplus_i Q_i$ to $\sum_i Q_i(u_i)$ . Since it was determined by a solution to the PDE, I know that the kernel contains any multiples of the defining equations. This means that the map

$\cdot P: D_{\mathbb{C}^n}^b\rightarrow D_{\mathbb{C}^n}^a$

given by premultiplication by the matrix $P_{ji}$ is killed by the map to $S$ .

Ah, but this characterization of solutions is sharp, because any map from $D_{\mathbb{C}^n}^a$ to $S$ which kills $\cdot P$ determines a solution of the PDE. To see this, notice that if I have such a map $f$ , then $u_i=f(\{0,...,1,...,0\})$ satisfies the PDE. Since two distinct solutions will give different maps, the solution space $S^P$ is exactly the equal to the subset of $Hom(D_{\mathbb{C}^n}^a,S)$ which kill the map $\cdot P$ .

This has a cleaner statement. The category of D-modules is an abelian category (it is the category of modules of a ring), and so the cokernel of any map exists. Let $M_P$ denote the cokernel of the map $\cdot P$ . By the definition of the cokernel, the maps in $Hom(D_{\mathbb{C}^n}^a,S)$ which kill $\cdot P$ are exactly given by $Hom(M_P,S)$ , so $S^P=Hom(M_P,S)$ .

However, the construction of $M_P$ had nothing to do with our specific choice of $S$ ; it only depended on the differential operators $P_{ij}$ . Therefore, if we can find $M_P$ , we can solve our PDE in all D-modules at the same time, by just looking at maps from $M_P$ into any given D-module. We say that $M_P$ represents the functor that sends a D-module $S$ to its set of solutions $S^P$ .

As Schnieders points out, this is a strong hint that $M_P$ is better to look at than the matrix of operators $P$ . This is because two different matrixes $P$ and $Q$ can determine the same set of solutions in every space, but then their corresponding D-modules $M_P$ and $M_Q$ must be isomorphic (by the Yoneda lemma).

The next question I’d like to answer is about solving inhomogenous PDEs. An inhomogeneous PDE in $S$ is given by differential operators $P_{ji}\in D_{\mathbb{C}^n}$ and $v_j\in S$ , with the goal being to find $u_i\in S$ such that

$\sum P_{ji}u_i=v_j$ .

Notice that if I have two solutions $\{u_i\}$ and $\{u'_i\}$ to the PDE, their difference solves the corresponding homogenous PDE,

$\sum P_{ij}(u_i-u'_i)=0$ ,

and so if one solution exists, I get all the rest by solving the homogenous PDE (one says that the solution space is a $S^P$ -torsor). Thus, the question of importance is not what the space of solutions looks like, but whether or not it has any solutions at all.

First, suppose I can find differential operators $Q_j$ such that $\sum Q_j P_{ji}=0$ . Such a collection of $Q_j$ determines an element in the kernel $N_P$ of the map $\cdot P$ from $D_{\mathbb{C}^n}^b$ to $D_{\mathbb{C}^n}^a$ (the most excellent map from before). Call such an element an algebraic compatibility condition.

Applying each $Q_j$ to one of the above equations, I get

$\sum_j Q_jv_j=\sum_i (\sum_j Q_jP_{ji})u_i=0$

Hence, for the PDE to have any hope of having solutions, the $\{v_j\}$ must satisfy all of the algebraic compatibility conditions; I will call a choice of such $\{v_j\}$ algebraically eligible.

However, these are just homogenous PDEs, which we just learned how to ‘solve’ (rather, how to characterize solutions to). Using similiar logic from before, we see that $Hom(I_P,S)$ is the space of algebraically eligible choices of $\{v_j\}\in S^b$ , where $I_P$ is the cokernel of the inclusion map from $N_P\rightarrow D_{\mathbb{C}^n}^b$ . Of course, this means that $I_P$ is the image of the map $\cdot P$ . As such, it fits into an exact sequence of D-modules

$0\rightarrow I_P \rightarrow D_{\mathbb{C}^n}^a\rightarrow M_P\rightarrow 0$ .

Applying the functor $Hom(-,S)$ to this sequence yields the following long exact sequence of derived functors:

$0\rightarrow Hom(M_P,S)\rightarrow S^a\rightarrow Hom(I_P,S)\rightarrow Ext^1(M_P,S)\rightarrow 0$

The first (non-trivial) arrow takes homogeneous solutions to themselves inside $S^a$ . The second arrow takes a collection of functions $\{u_i\}$ to $\{P_{ji}u_i\}$ , thought of as defining a choice of $\{v_j\}$ which is algebraically eligible (this is how we think of elements in $Hom(I_P,S)$ ). Therefore, $Ext^1(M_P,S)$ is the group of algebraically eligible choices of $\{v_j\}$ modulo those $\{v_j\}$ which actually have solutions.

Thus, if I have an inhomogenous PDE, I first check if the choice fo $\{v_j\}$ is algebraically eligible. Then, I find its image in $Ext^1(M_P,S)$ via the above map, and if it vanishes, then I know my inhomogenous PDE has a solution.

This is further evidence that $M_P$ is the right guy to look at. Not only can he parameterize solutions to the homogenous PDE, but he can also detect whether or not a corresponding inhomogenous PDE has a solution. Hopefully, this was a first step in convincing you that D-modules are a good framework in which to think about problems of this form.

I still have plenty of fun stuff on the to-do list. First, I should sheafify this whole construction so that everything above works for PDEs on arbitrary complex manifolds. I should also show how many fun things in differential geometry can be stated in this language, like connections on a bundle. I also will indulge my algebraic geometry roots and show how you can define differential operators on any scheme. Oh, and of course I should mention important theorems, lest ye think that D-modules are nothing more than a pretty framework in which to state problems.

Tags: math.AC

This entry was posted on September 6, 2007 at 5:36 pm and is filed under Basic Grad Student, Greg. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

9 Responses to “D-module Basics I”

“Everything” about D-Modules « The Unapologetic Mathematician Says:
September 6, 2007 at 9:14 pm | Reply
[…] Over at The Everything Seminar, Greg Muller has a great introductory post about D-modules, which is what representation theory and category theory have to do with partial differential […]
John Baez Says:
September 7, 2007 at 3:42 pm | Reply
Go for it! I keep meaning to learn more about D-modules and then explain them to the world. You beat me to it.

Will you eventually explain the derived category version of the Riemann-Hilbert correspondence? That’s on my wish list. But never mind – I’ll take what I can get.
Michael Kinyon Says:
September 7, 2007 at 10:10 pm | Reply
You might also find Dragan Milicic’s old notes useful:

http://www.math.utah.edu/~milicic/

Scroll down a bit, and you’ll find them.
Greg Muller Says:
September 8, 2007 at 2:32 am | Reply
I really have no plan for how far I am going to go… I would hope to get to the non-derived Riemann Hilbert correspondence before I peter out; otherwise, this will have been a hollow exercise in finding pretty ways of saying hard problems. I would love to learn and explain the derived version, but that will depend on the ambient interest level and my free time.
Scott Carnahan Says:
September 8, 2007 at 7:17 pm | Reply
Sorry if I’m jumping the gun, but how do you define differential operators on a non-smooth scheme?
Greg Muller Says:
September 9, 2007 at 2:44 am | Reply
I know what you are getting at, Scott, and I mention it in the second part of this series. For non-smooth affine schemes, the usual abstract notion of differential operator still works. However, the technique everyone seems to use for localizing differential operators is to do it for derivations and then appeal to smoothness.

In short, I don’t how to make it work, if it can be made to work. However, the idea I had to try (which is too late to pursue at the moment), is the following.

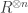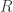A differential operator $\delta$ of order n on $\mathbf{Spec}(R)$ defines a linear map from $R^{\otimes n}$ to $R$ by
$a_1\otimes a_2\otimes...\otimes a_n \rightarrow [...[,[\delta,a_1],a_2]...,a_n]$

This map has lots of nice properties, including that it is a derivation in each argument. This implies that, if $f$ is some element on whose inverse I would like to operate, I have identities like
$f[...[,[\delta,f^{-1}],a_2]...a_n]=-f^{-1}[...[,[\delta,f],a_2]...a_n]$
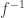The question is then, can we use the above data alone to define an action of $\delta$ on $f^{-1}$ ?
mackeeper Says:
September 25, 2011 at 6:24 pm | Reply
mac keeper scam…

[…]D-module Basics I « The Everything Seminar[…]…
hickman family from missouri Says:
May 13, 2015 at 12:30 pm | Reply
hickman family from missouri

D-module Basics I | The Everything Seminar
Phillip Harmsworth Says:
October 20, 2020 at 5:17 am | Reply
Schneiders’ notes are now at: http://www.analg.ulg.ac.be/jps/rec/idm.pdf