We’ve had some fun on the blog recently talking about divergent series and assigning bizarre but appropriate sums to them. However, I have a bit of a pet-peeve about when people try to mis-use infinite series to make real-world predictions.
My favorite example comes from a heated argument I had with a friend about a problem from his Probability class. He had the following homework problem.
A casino opens a game that plays as follows. A person pays 1,000 dollars to play, and then they get to flip a coin until they it comes up tails. The pay-out is
dollars, where n is the number of heads that came up in a row. Is this game worth playing?
The mathematical approach is to compute the expected value, which is the sum of every possible payoff times the chance of that payoff. The possiblities correspond to the number of heads; the possiblity of getting exactly n heads is , while the payoff is
dollars. Therefore, the expected value is
forever, so it’s infinite! Hooray! Then the game is worth playing, and it would be no matter how much it costs to play.
Of course, a few days later, all the formerly giddy mathematicians involved are broke and confused. What went wrong?
There are actually several things wrong with the above logic, but the one that bothers me most is the sheer naivity in assuming that there are really an infinite number of terms in computation of expected value.
Every math word problem like the one above comes with implicit assurances that real-world factors don’t enter in (for instance, almost every logic puzzle in the world involves only participants with infallable logical faculties). However, consider the fantastically large payoffs involved in the game. Is the casino really going to pay you 2^1000 dollars? Of course not, such a number is absurdly larger than the number of atoms in the visible universe. And yet, such payouts play a crucial role in the computation of expected value. If the casino was allowed to file for bankruptcy and not pay out rewards of 2^1000 dollars or greater (but still somehow paid all smaller astronomical totals), then the expected value of the game is only 999 dollars, and so the game wouldn’t be worth it.
How can anyone, even in the mathematical abstract, claim a solution that doesn’t stand up to the flimsiest application of reality? This is just a problem in a textbook, but I have repeatedly heard people discuss a similar betting strategy as if it was possibly legitimate. Start with a fair game with a half chance of doubling your bet, and a half chance of losing your bet. Bet an initial amount , and if you ever win, stop betting. If you lose, instead of quitting, double your previous bet and play again. The narrow-minded mathematical claim is that you are guaranteed to make
dollars this way.
The proof of this spurious claim is simple, and very similar to the previous computation. If you lose times in a row and then win, your winnings are
. Also, you must win at some point, since the chance of you losing
in a row approaches zero very fast. Therefore, you always win
dollars.
Before another round of enterprising mathematicians lose their nestegg, lets debunk this. The fallacy here is that, instead of the casino having a finite amount of money, the player has a finite amount of money. For this strategy to work, the casino must allow you to make these geometrically increasing bets without bound. At some point, the casino has to cut you off and then take everything of value from you. What ends up happening is that, most of the time you make dollars, and a very small fraction of the time you lose everything you have; and it happens in such a way that the net probabilistic gain is zero (its a fair game, after all). So, in reality, instead of beating the casino, a large number of possible versions of yourself are ganging up and mugging one unlucky possible version of yourself. (Probablity is always more fun when you imagine self-on-self violence across possiblity space.)
While I’m at it, I want to mention another reality-based fallacy that I think crops up in idealistic math problems of value, as well as in people’s actual risk-reward estimates. The trick is that ‘a dollar’ is not equally valuable to all people at all times. Even with lifestyle and personality aside, people value the gain of a dollar less the more money they already have. That means that the value of some money is a non-linear function of the total amount of money.
The point is that, factoring for this, even ‘fair games’ might not be fair. Given a half chance of losing a dollar and a half chance of gaining a dollar, the expected value could easily be less than the original value. This is easier to see with a very large bet on a fair game. Say you have 5,000 dollars in the whole world, is it worth it to bet all 5,000 on even a fair game? Half the time you end up completely destitute, and the other half you end up with 10,000 dollars, which isn’t so much better than 5,000 dollars. On a much, much smaller scale, even one dollar fair bets can be not worthwhile (though on a microscopic scale). This model punishes pretty much all fair risk, and so it breaks most problems of this type.
Tags: math.PR
September 3, 2007 at 11:08 pm |
The homework problem, by the way, is known as the “St. Petersburg paradox”:
http://en.wikipedia.org/wiki/St._Petersburg_paradox
Bernoulli, who originally proposed the problem, also proposed a theory of utility similar to what you discuss here, although this does not, I think, really get at the heart of the matter. As with most puzzles involving infinity, one has to look at the behaviour of the finite truncations of the infinite object in order to really see what is going on. Also, using expectation alone as the measure of utility only makes sense when there are enough trials that the law of large numbers kicks in (and in the case of the St. Petersburg paradox, one needs an exponentially large number of trials to get the average payoff above any given level). Before then, utility is not really expressible as a scalar deterministic quantity.
September 4, 2007 at 12:49 am |
Also, if you’re discussing utility, it’s probably the log of the expected value that is relevant (which makes the utility dwindle rapidly). this goes back to Von Neumann-Morgenstern games.
September 4, 2007 at 3:17 am |
Personally, the introduction of the notion of utility does not seem to be a satisfactory solution. It seems more like a solution to a problem. I mean, what is the semantic of infinite expectation in the case? I’ve got a feeling that this has something to do improper distributions but couldn’t quite pin it down exactly.
September 4, 2007 at 4:54 am |
A small correction. Paragraph 3. It is not 1+1+1… It is 1/2+1/4+1/8+… This is because if you win on nth step you have to subtract the money you’ve lost (2^n-1) during the previous n-1 steps. So you get 2^n-(2^n-1)=1
September 4, 2007 at 12:56 pm |
Thanks for the extra info! I have often found the notion of utility fascinating, but I also question the ability and usefulness of trying to model it mathematically. Mostly it is helpful in refuting the accuracy of mathematical solutions; trying to assign a function from amounts of money to utility should rightly dissolve into a hopelessly complicated analysis of happiness and wealth.
Anton, I’m not sure I follow your point. You don’t lose any money while playing the game, except for the initial entry fee which doesn’t affect the expected value computations. That is however, the correct computation for the ‘double after a loss’ betting strategy, since the payoff after the win is the same, except you lose money at each of the previous steps
September 4, 2007 at 11:56 pm |
One can more or less eliminate the role of subjective factors such as happiness from utility computations if one assumes the existence of a large, liquid, and frictionless market in which one can trade away various risks.
Consider for instance the value of a lottery ticket which is guaranteed to pay X dollars with probability 1/N, and pay nothing otherwise. One can argue that the value of this ticket to any particular person may be larger or smaller than the expected value of X/N because of variations in the utility function. But suppose that one has a syndicate which has in excess of X dollars in assets. Then this syndicate can buy up every lottery ticket it can get its hands on for any price significantly less than X/N, and be pretty much assured of a profit thanks to the law of large numbers. Because of this, there is a floor as to the price of this lottery ticket which is basically X/N. Conversely, the syndicate can use its assets to sell up to N lottery tickets for any price greater than X/N and also be fairly well assured of a profit; thus there is also a ceiling to the price of this ticket which is also basically X/N. So, in the presence of a frictionless market, we can say that the value of this ticket is indeed close to its expected utility. (In practice, friction and regulation prohibit this analysis from working perfectly, but the basic point remains that a sufficiently large market can set a deterministic price to an object of probabilistic value.)
Incidentally, with this analysis, the value of the St. Petersburg game is roughly comparable to the logarithm of the size of the market one can trade that game in, or the logarithm of the size of the casino, whichever is smaller.
September 5, 2007 at 2:32 am |
Reminds me of “volatility pumping,” which I was just reading about in David Luenberger’s excellent book Investment Science (pg 422)
Suppose you have two bets available: one is a stock that either doubles or reduces by 1/2 each time period, each with probability 50%; the other is an investment that does nothing — it just returns your investment.
Neither investment by itself has an overall growth rate, but in combination it’s possible to make money by rebalancing each period to have half your money in each asset, with an expected gain of about 6% per period.
September 5, 2007 at 7:51 am |
This is obviously a problem in mathematical finance. Well it’s at least a problem for anyone who would want to use mathematical finance to make money. You don’t really mind winning an arbitrarily large sum of money, but there is something wrong with losing a whole lot. There is a concept called -admissibility which basically says that your change in wealth is bounded below. Specifically, if
-admissibility which basically says that your change in wealth is bounded below. Specifically, if  is a semimartingale (say the price of some risky asset), and
is a semimartingale (say the price of some risky asset), and 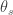 is a predictable strategy, then
is a predictable strategy, then  is
is  admissible for some
admissible for some 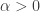 if
if 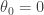 and
and  for all
for all 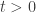 . Admissible means it’s
. Admissible means it’s  -admissible for some
-admissible for some  . Basically, with an admissible process, you can win as much as you want, but you can’t lose arbitrary amounts of money. At the very least, admissibility fixes the doubling strategy and this game you’ve described above. Although you can stilll no doubt define processes which will allow you to win arbitrary amounts of money. Unfortunately those processes have very short lifespans on the stock market.
. Basically, with an admissible process, you can win as much as you want, but you can’t lose arbitrary amounts of money. At the very least, admissibility fixes the doubling strategy and this game you’ve described above. Although you can stilll no doubt define processes which will allow you to win arbitrary amounts of money. Unfortunately those processes have very short lifespans on the stock market.
September 5, 2007 at 8:11 pm |
yeah I guess I should have said ‘At the very least, admissibility fixes the doubling strategy but not the game you described above.’
Also, a few years ago, Pepsi had a promotion where if you got a thing under the bottle cap, you got to go to florida or something and be eligible to make it into a drawing of ten people. In the drawing, you would be assigned a number 1-1000. Drew Carey would come out with a monkey (himself) which would pick balls at random from a bucket of 1000 numbered balls. Whoever was closest won 1000000 bucks. If it matched the number assigned to you exactly, you would win a billion dollars. Of course it was paid over the course of 50 years or something, and you got 500 million on the 50th year. I’m still curious if it was rigged, though. While their expectation is still the same, it seems like unnecessary added risk for their promotion and a billion dollars is a crapload of money, even if it is unlikely (1% is still 1%)
October 1, 2007 at 5:44 am |
[…] Infinite Series vs. Reason […]
October 1, 2007 at 5:45 am |
[…] Infinite Series vs. Reason « The Everything Seminar […]
October 25, 2008 at 2:49 am |
tickets…
tickets…
April 30, 2010 at 7:53 pm |
[…] the bad math behind a classic gambling scheme that’s “guaranteed” to pay off, in Infinite Series vs. Reason. Specifically, if you are, say, flipping a coin to determine whether you win a bet, and you double […]
January 19, 2011 at 10:21 am |
that of a good read.
September 24, 2013 at 10:27 am |
Fabulous, what a website it is! This website
presents useful data to us, keep it up.
September 16, 2014 at 12:11 am |
I believe what you published made a bunch of sense.
However, think about this, what if you typed a catchier
post title? I ain’t saying your content is not good., however what
if you added a title to maybe get folk’s attention? I mean Infinite Series vs.
Reason | The Everything Seminar is a little plain. You might peek at Yahoo’s home page
and watch how they create post titles to get people to open the links.
You might try adding a video or a picture or two to get
people interested about everything’ve got to say. Just my opinion,
it could bring your website a little livelier.
December 2, 2021 at 7:38 pm |
winning in Slots
Infinite Series vs. Reason | The Everything Seminar