Surfaces and Spinors

by mnoonan

A huge problem that many people initially have with differential geometry is over-representation. Manifolds are conventionally defined via absurdly large, Zorn’s-lemma’d maximal atlases, giving an enormous sea of possible coordinates which could represent an object. Maps with some property from one surface to another are often defined relative to local charts, involving many arbitrary choices of coordinates, covers, and so forth. Tensor fields might be built up as collections of numbers with absurd transformation rules. In that mass of symbols, where is the geometry?

Conversely, who would expect upon first inspection that the trace and the determinant of a matrix are coordinate-invariant quantities? What about the Riemann curvature tensor? Would you have seen that the Gaussian curvature is intrinsic, yet the mean curvature is extrinsic? Can you identify the Willmore energy as invariant under Mobius transformations, despite being constructed from Euclidean invariants? What if it was written in local coordinates?

This overabundance of representations in differential geometry is a mixed blessing. They give us a thousand ways to look at a problem, but 995 of those obscure the geometric features we are trying to understand. Ideally, we would like to have a language for geometry which is rich enough that we can efficiently describe and compute with geometric objects, yet weak enough that we cannot state non-geometric facts. This might be a bit much to ask in general, but many big advances in differential geometry have come through finding clever representations for certain classes of geometric objects which allow us to easily read off or insert geometric information. At Greg’s request, I’d like to share a modern version of one of the classical representation theorems in the geometry of surfaces.

Today, I want to write about a modern generalization of the Weierstrass representation of minimal surfaces. This give us a way of representing minimal surfaces using meromorphic data, providing a bridge between the geometry of minimal surfaces and complex analysis. This bridge is almost entirely responsible for our expansive knowledge on minimal surfaces. It is hard to think of a PDE in geometry that we know more about. Research on a closely related subject (surfaces of constant mean curvature) languished for almost 150 years until a Weierstrass-type representation was recently found.

Way back in the ancient history of this blog, I wrote a post about how minimal surfaces don’t come alone, but actually live in one-parameter families. The critical observation is this: if $f : M \rightarrow \mathbb{E}^3$ is a conformal parametrization of a minimal surface then both $df$ and $*df$ are closed. By mixing them together, we can create a whole family of minimal surfaces. This is fantastic, but constructing differential forms that are both closed and co-closed is a little tricky. It clearly has a close relation to Hodge theory, where we attempt to find forms which satisfy $\Delta \omega = 0$ and then go on to prove that such forms are both closed and co-closed. So the differential of a conformal parametrization of a minimal surface seems to be “harmonic” in some important sense. We know that harmonic things like to be the real parts of holomorphic things — maybe we can utilize this to tie minimal surfaces to complex analysis?

Weierstrass found just such a relationship in the mid-nineteenth century: if $\omega$ is a holomorphic differential and $g$ is a meromorphic function (both on $\mathbb{C}$ ) such that $\omega$ has at least two zeros whenever $g$ has a pole (everything counted with multiplicity), then the function

$F(z) = Re \int_{z_0}^z (\frac{1-g^2}{2}, i\frac{1 + g^2}{2}, g) \omega$

is a conformal parametrization of a minimal surface in $\mathbb{E}^3$ . Furthermore, every minimal surface parametrized by $\mathbb{C}$ is of this form. This representation is like a gift that has kept on giving for the last 150 years. Even very recently, minimal surfaces with new properties have been discovered via this representation. It has only two drawbacks: is annoyingly asymmetric in $\omega$ and $g$ with bothersome zero/pole relations that we have to deal with, and it does not globalize well. Because of this last drawback, it has been somewhat harder to talk about minimal surfaces with nontrivial topology.

Instead of going into the Weierstrass representation in more detail, let us change our perspective and try to reinvent it ourselves. I am going to describe a version of the Weierstrass representation first proposed by Dennis Sullivan and developed thoroughly by Kusner and Schmidt. First, let us think about what it means for a function $f : M \rightarrow \mathbb{E}^3$ to be conformal (where $M$ is now an arbitrary Riemann surface) . Conformal is almost synonymous with holomorphic, so consider the $\frac{\partial}{\partial {z}}$ derivative of $f$ (this works with the $\bar{z}$ derivative too):

$f_{z} = \frac{1}{2}(f_x - i f_y)$

This is some function now from $M$ to $\mathbb{C}^3$ . It isn’t zero, but if $f$ is conformal then it does have zero norm under the complexified dot product:

$|f_{z}|^2 = \frac{1}{4}(|f_x|^2 - |f_y|^2 - 2i f_x \cdot f_y)$

So now we have a nice lemma: a map to $\mathbb{E}^3$ is conformal iff the $\frac{\partial}{\partial {z}}$ derivative lies on the lightcone $C = \{ \psi \in \mathbb{C}^3 : |\psi|^2 = 0\}$ . Equivalently, the (1,0)-differential $\partial f = f_z dz$ must take values in $C$ .
Can we go the other way? Given a form $\omega \in \Omega^{(1,0)}_M(C)$ , when can we recover $f$ ? We don’t actually need $\omega$ to be closed for this. A short computation shows that it is sufficient that $Re d\omega = 0$ .

Now we just need to understand maps taking values in the lightcone $C$ . Can we describe $C$ in some nice way? If we think of $\mathbb{C}^3$ as the tautological bundle over $\mathbb{CP}^2$ , then $C$ is the tautological bundle over the variety defined by $x^2 + y^2 + z^2 = 0$ . We can explicitly parametrize this variety with a copy of $\mathbb{CP}^1$ :

$V_2([x : y]) = [ x^2 - y^2 : i(x^2 + y^2) : 2xy]$

Incidentally, I chose this name because it reminds me of Veronese variety coming from the Veronese embedding $V_2 : \mathbb{CP}^1 \rightarrow \mathbb{CP}^2$ . I can’t put my finger on the exact relationship, though. Can all of you algebraic geometers lend me a hand here?

Ok, so here is what we have done so far. We found a relationship between conformally parametrized surfaces in $\mathbb{E}^3$ and maps to the lightcone in $\mathbb{C}^3$ . This lightcone is the embedding of the tautological bundle $\Sigma \mathbb{CP}^1$ which sits over the Riemann sphere $\mathbb{CP}^1$ . So every map to $C$ can also be described as a map to $\Sigma \mathbb{CP}^1$ .

Remember, to construct a surface we actually want a 1-form with values in $C$ . Since the embedding $V_2$ is of degree 2, that means that $x$ and $y$ need to be of the form $x = \psi_1 \sqrt{dz}, y = \psi_2 \sqrt{dz}$ . That is to say, we want a pair of sections $\psi_i \sqrt{dz}$ of some spin bundle $S$ on $M$ : a bundle such that $S \otimes S = K$ . Given such a pair, we may construct a form of type $\Omega^{(1,0)}_M(C)$ . This form will be integrable to a surface only when its differential has vanishing real part (see above).

From this spinor pair you can read off all sorts of geometric information about the corresponding surface. The normal map is given by the ratio $\psi_1 / \psi_2$ . If we combine the two spinors into a vector of spinors $\Psi = (\psi_1 \sqrt{dz}, \psi_2 \sqrt{dz})$ then the area form is just

$A = 4 |\Psi|^2 = 4(|\psi_1|^2 + |\psi_2|^2) |dz|^2$

The mean curvature is

$H = \frac{\Psi \cdot \bar{\not \partial \Psi}}{|\Psi|^4}$

where $\not \partial$ is the Dirac operator.

More interesting, however, is the fact that we can also read off gross topological information about the surface from this data! For most Riemann surfaces, there are many spin bundles (in the compact case, $2^{2g}$ of them). Kusner and Schmidt show how the Arf invariant of the resulting surface may be read directly from the choice of spin bundle! This means we can determine if our surface will be regularly homotopic to an embedding simply by looking at which spin bundle we pulled $\Psi$ from. This sort of large-scale control is really uncommon and exceptional in differential geometry.

To wrap up, let me actually say a little bit about how this relates back to the Weierstrass representation. The key is to figure out exactly what the integrability condition is in terms of $\Psi$ . Kusner and Schmitt show that $\Psi$ describes a surface if and only if it satisfies the differential equation

$\not\partial \Psi = H |\Psi|^2 \Psi$

If you combine this with the previous equation for $H$ , you see that the right-hand side of this equation is just the projection of the conjugate of $\not \partial \Psi$ onto $\Psi$ . In the special case of minimal surfaces ( $H = 0$ ), this reduces to the equation $\not \partial \Psi = 0$ , which simply says that the spinors are meromorphic. This gives us the global, symmetric version of the Weierstrass representation: “There is a 1-1 correspondence between conformal parametrizations $f : M \rightarrow \mathbb{E}^3$ of minimal surfaces and pairs of meromorphic sections $\Psi \in S \oplus S$ of spin bundles over $M$ .”

Given two such spinors $\psi_1 \sqrt{dz}, \psi_2 \sqrt{dz}$ the corresponding Weierstrass representation is

$f(z) = Re \int_{z_0}^z (\psi_1^2 - \psi_2^2, i(\psi_1^2 + \psi_2^2), 2\psi_1 \psi_2) dz$

To recover the classical Weierstrass representation, define $\omega = (\psi_1 \sqrt{dz})^2$ and $g = \psi_2 / \psi_1$ .

Tags: math.DG

This entry was posted on September 28, 2007 at 2:18 pm and is filed under Basic Grad Student, Matt. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

6 Responses to “Surfaces and Spinors”

mister e Says:
September 28, 2007 at 7:07 pm | Reply
What you are describing (the interplay between the geometry of Weierstrass minimal surfaces and O(1)->P^1) is an application of (mini)twistor theory.

See Hitchin’s papers on monopoles in the early 1980s for a very beautiful exposition.
Michael Kinyon Says:
September 28, 2007 at 8:45 pm | Reply
The first three paragraphs of this post are one of the best adumbrations I have seen of the adage “differential geometry is the study of properties that are invariant under change of notation”.
David Speyer Says:
September 28, 2007 at 9:31 pm | Reply
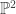Regarding the Veronese embedding: The Veronese embedding of $\mathbb{P}^1$ into $\mathbb{P}^2$ is given by

$(t:u) \mapsto (t^2:tu:u^2).$

The image is xz=y^2.. Making the change of coordinates x=(x’+z’), z=(x’-z’), this becomes (x’)^2=y^2+(z’)^2, which is parameterized by (x’,y,z’)=(t^2+u^2, 2tu, t^2-u^2). (Fans of recreational number theory may recognize this as the standard parametrization of pythagorean triples.) Throwing an i in front of the x’ coordinate to switch the sign of (x’)^2 gives your paramterization.
mister e Says:
September 29, 2007 at 6:52 am | Reply
What you are talking about is essentially (mini)twistors theory.
This week in the arXivs… « It’s Equal, but It’s Different… Says:
September 29, 2007 at 8:35 am | Reply
[…] Surfaces and Spinors […]
Daniel Says:
February 7, 2009 at 8:24 pm | Reply
Most of this is way beyond me – Im an architect by trade, but I’ve been fascinated by these ideas ever since I encountered Needham’s Visual Complex Analysis. I’ve been developing some ideas about possible architectural uses of a type of surface made using solutions to Laplace’s equation. You can see them here:

Rheotomic Surfaces

I’ve also been wondering about the combination of these with some other stuff on rotations of the 3-sphere:

4-Dimensional Rotations

Maybe you could take a look and tell me if I’m talking nonsense. hopefully you might enjoy some of the visualisations too