Antisymmetry in Geometry, I

by mnoonan

Isabel’s post at God Plays Dice asking for a geometric entity realizing the dot product got me thinking again about a question that my friend Ron asked me several years ago: “Why do geometers always focus on antisymmetric tensors and ignore the symmetric ones?”

It certainly seems that antisymmetric objects have more grit to them — they correspond to things like fields of infinitesimal k-planes, or symplectic structures, or fluxes. Things you can imagine getting your hands on. Symmetric objects, on the other hand, are things like Riemannian metrics and the dot product, or the shape operator. They seem to measure things, which is far more subtle than being things. I’m always happier with a 2-form over a quadratic form: I can see the former.

There is a lot to say about this subject, and exploring it could take us to some fun places. As a first step in that direction, I’d like to share a proof that every manifold admits a metric which may be new to you.

One of the most-used tools in the differential geometry kit is the epic-sounding partition of unity. These let us glue things defined on a small-scale into things defined over your whole manifold, making many problems in geometry solvable by the schema “1.) do a thing locally, then 2.) glue it up using partitions of unity into a global thing”. Incidentally, the absence of holomorphic partitions of unity is what makes local/global problems on complex manifolds far less trivial than on smooth real manifolds. This is entirely responsible for the differences between the theory of smooth manifolds and the theory of complex manifolds.

The first serious application of partitions of unity is usually to prove that every manifold admits a nonvanishing symmetric 2-form — in other words, a Riemannian metric. The proof is easy once you can build and run the (nontrivial!) partition of unity machine: split your manifold up into chart domains, pull back the dot product on $\mathbb{R}^n$ to get local metrics, glue them up into a global metric. There are details which I will happily ignore, because I want to talk about a different proof.

The previous proof is excellent for getting used to working with partitions of unity. However, it gives some false intuition. We should be surprised that every manifold admits a metric. Here’s why: a Riemannian metric is a nonvanishing symmetric 2-form on $M$ . By analogy, consider an ANTIsymmetric 2-form on $M$ . The kernel of this 2-form then defines a nonvanishing $(n-2)$ -plane field on $M$ . The world-famous hairy ball theorem tells us that many manifolds fail to admit nonvanishing vectorfields. Why would we expect them to admit nonvanishing $(n-2)$ -plane fields?

In fact, if $X$ is a nonorientable 2-manifold then it must not admit any nonvanishing 2-form fields, since a nonvanishing 2-form field would give $X$ a consistent orientation. So many manifolds will fail to admit nonvanishing antisymmetric 2-form fields — why would be expect them to admit nonvanishing symmetric 2-form fields?

Here is a fundamentally different proof which hopefully sheds a little more light on the subject, if you know your bundles. Consider the space $FM$ of frames on $M$ . A point in $FM$ is a pair $(p, B)$ where $p$ is a point of $M$ and $B$ is an ordered basis of the tangent space to $M$ at $p$ . This is a principal $GL(n)$ -bundle over $M$ . Picking a metric on $M$ is the same thing as saying which of these frames should be considered orthonormal. The different choices of “orthonormal” we could make at a point are parametrized by $GL(n) / O(n)$ . So to pick a set of frames to call orthonormal over all of $M$ , we need to find a section of the bundle of orbits $FM / C^\infty(M,O(n))$ .

Now, most bundles just don’t have global sections. However, the Gram-Schmidt process gives us a retraction of $GL(n)$ onto the subgroup $O(n)$ , so the quotient $GL(n) / O(n)$ is homotopy-equivalent to a point. This means that there are no nontrivial bundles with fiber isomorphic to $GL(n) / O(n)$ . We can always find a global section.

But then we are finished! A section of $FM / C^\infty(M,O(n))$ is the same as choosing an $O(n)$ -orbit of frames at each point, which is the same a metric. The fact that $GL(n)$ retracts onto $O(n)$ means that $FM / C^\infty(M,O(n))$ must be a trivial bundle. It therefore admits a global section, corresponding to a global Riemannian metric.

This phenomenon (symmetric data retracting away, leaving only topologically interesting antisymmetric data) appears in other places, and might be lurking behind our difficulties in realizing symmetric objects geometrically. More on these “other places” some “other time”.

This entry was posted on September 13, 2007 at 12:08 am and is filed under Basic Grad Student, Matt. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

15 Responses to “Antisymmetry in Geometry, I”

Caroline Says:
September 13, 2007 at 5:42 am | Reply
Hey there,

This is Caroline from SocialRank.

I am trying to get in touch with you but couldn’t find your email address.

We will index your blog posts as part of our content filter. I’d like to send you an invite to a beta preview of our new Web 2.0 site.

Can you get back to me with your email address.

Mine is caroline@mathbloggers.com

Kind regards,

Caroline

http://www.SocialRank.com
John Armstrong Says:
September 13, 2007 at 9:46 am | Reply
Can you flesh out that point about the Gram-Schmidt process? Something about it just isn’t sticking in my brain. How does it give that retraction?
mnoonan Says:
September 13, 2007 at 10:19 am | Reply
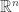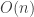Sure thing, John. I want to choose a reference orthonormal basis $e_i$ of $\mathbb{R}^n$ so that I can think of elements of $GL(n)$ as ordered bases and elements of $O(n)$ as ordered orthonormal bases. So given a basis $B$ , think about how Gram-Schmidt is applied: first, we normalize $B e_1$ . Instead of imagining this as a discrete action, gradually scale $B e_1$ until it is normalized. Then move on to $B e_2$ : make it orthogonal to your last vector by gradually removing the projection, then normalize by gradually scaling it. And so on, continuously removing projections and scaling the result.

Altogether, this gives a deformation retract taking any element $B \in GL(n)$ continuously to the corresponding Gram-Schmidt basis $B_{GS} \in O(n)$ .
John Armstrong Says:
September 13, 2007 at 10:52 am | Reply
Okay, looking at it as a deformation makes more sense now.

So how does the picture change if I want to move from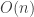 $O(n)$ to $O(p,q)$ ? That is, what obstruction (if any) is there to the existence of a pseudo-Riemannian metric of a given signature?
Ben Webster Says:
September 13, 2007 at 11:06 am | Reply
John-

It’s a more general theorem that all reductive algebraic groups over the reals contract onto their maximal compact subgroups. The magic words are Iwasawa decomposition, which shows that every such group is the product (topologically) of the maximal compact, and a unipotent subgroup, which is necessarily contractible.
Aaron Bergman Says:
September 13, 2007 at 11:15 am | Reply
The existence of a Lorentzian metric (ie, signature (1,p)) is equivalent to the existence of a global direction field. In other words, a field of unordered pairs {-v,v}. As I recall, in the compact case that’s equivalent to the vanishing of the Euler character.
Ben Webster Says:
September 13, 2007 at 11:17 am | Reply
Of course, there’s a second proof that $GL(n)/O(n)$ is contractible, which is easier, IMHO (and secretly the same as the proof by partitions of unity).

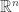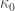One can obviously identify $GL(n)/O(n)$ with the set of inner products on $\mathbb{R}^n$ . Let $\kappa_0$ be your favorite inner product, and consider the map on the set of inner products times $[0,1]$ sending $(\kappa,t)\mapsto t\kappa+(1-t)\kappa_0$ . This is the identity at 1, and the map to a point at 0, and an inner product at every point (since the sum of inner products is an inner product, which is also what makes the proof using partitions of unity go).
Ben Webster Says:
September 13, 2007 at 11:30 am | Reply
That is, what obstruction (if any) is there to the existence of a pseudo-Riemannian metric of a given signature?

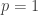There are obstructions (as Aaron pointed out). The existence of such a form is equivalent to the $O(n)/(O(p)\times O(q))$ -bundle associated to the tangent bundle having sections. In the case where $p=1$ , this bundle is the projectivization of the tangent bundle (hence the theorem Aaron mentioned). In general, it’s just going to get nastier. You’re going to get some relations on characteristic classes (coming from the kernel of the pullback map on cohomology $H^*(BO(n))\to H^*(B(O(p)\times O(q)))$ ), but I’m not sure if those will be sufficient.
mnoonan Says:
September 13, 2007 at 11:31 am | Reply
In general, to get a metric of signature $(p,q)$ you need to globally splitting of each tangent space into a product of a p-plane and a q-plane (unoriented). Given such a splitting, you can then proceed to name your favorite nondegenerate metrics on each plane field as above to construct a global metric of signature $(p,q)$ . Since not every manifold admits an unoriented p-plane field, it is not always possible to construct a nondegenerate $(p, n-p)$ -metric.

In terms of reducing the structure group of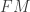 $FM$ , the splitting of $TM$ corresponds to a reduction of the $GL(n)$ structure group to a $GL(p) \times GL(q)$ structure group, which is only possible if we can find a global section of $FM / GL(p) \times GL(q)$ . You can see the space of p/q splittings floating around in the Grassmannian fibers $GL(n) / GL(p) \times GL(n-p)$ of this bundle.
Terence Tao Says:
September 13, 2007 at 1:14 pm | Reply
I think it is not so much the symmetry that makes things topologically uninteresting as the positivity. The cone of positive-definite Riemannian metrics on a manifold is, well, a cone: the sum of two Riemannian metrics is again a Riemannian metric, which is why partition of unity tricks work so well here: cones are topologically uninteresting. In contrast, the sum of two non-degenerate 2-forms (say) is not necessarily non-degenerate. (Ben’s comment above is saying much the same thing.)

If one were to look at Lorentzian metrics rather than Riemannian, then even though there is symmetry, there is still a topological obstruction, as Aaron and others have already pointed out.

Things which are positive, such as Riemannian metrics, positive measures, and norms, are not as manifestly geometric as, say, differential forms, because they are now also encoding some analysis (magnitudes, lengths, bounds, inequalities, etc.) as well as geometry.
Deane Yang Says:
September 16, 2007 at 12:43 pm | Reply
I’d like to say what’s already implicit in earlier comments:

In the original text, you define a Riemannian metric to be a nonvanishing symmetric 2-form. This is not right. The symmetric 2-form must be positive definite and not just nonvanishing.
Wowow Says:
December 26, 2014 at 11:40 am | Reply
Interseting article… but its too hard formula. according to me…
Jaya Corps Says:
December 31, 2014 at 4:59 am | Reply
i like this article
madu diet ath thoifah Says:
May 17, 2018 at 2:35 am | Reply
thank you for sharing this article
prof dr mircea orasanu Says:
June 5, 2019 at 11:08 am | Reply
these appear in many situations as observed prof dr mircea orasanu and orof drd horia orasanu and followed for important that are valuable in conformal transforms and LAGRANGIAN OPERATORS