I have been reading recently about complex dynamics, in particular the Mandelbrot set and the associated Julia sets. Mathematicians seem to be in awe of these fractals, in particular of the intricate beauty of the Mandelbrot set, and introductions to the subject tend to focus on the stunning complexity of the (computer-generated) pictures.
Though I agree that the pictures are compelling, I think it does a disservice to the subject to focus on the complexity. In some sense, Julia sets are quite straightforward, not really much more complicated than the Sierpinski gasket or the Koch curve. The structure is just a little bit harder to see, primarily because a Julia set is something like a “co-fractal”.
Fractals vs. Co-Fractals
The term “fractal” is notoriously hard to define. Mandelbrot used the term to refer to any set with fractional Hausdorff dimension, but he admitted that this was not a very good definition — it captures the complexity of a fractal, but not the self-similarity. The Wikipedia article on fractals gives a list of five criteria that a geometric object must satisfy to be considered a fractal, but it doesn’t even try to make these criteria precise.
The simplest fractals are those that are self-similar, meaning that they are constructed of one or more copies of themselves. Here are some examples:

Each of these fractals contains several scaled-down copies of itself (three for the gasket, eight for the carpet, and four for the Koch curve). More precisely, each self-similar fractal
comes with a finite set of embeddings
, whose images cover all of
.
Now consider some Julia sets:
Just to be clear on terminology, the Julia set is the fractal boundary between the black region and the colored region. As you can see, it is a sort of infinite graph, with loops connected to loops connected to other loops. The structure, however, seems much more complicated than for the previous set of fractals. Though they certainly have repeating patterns, none of these Julia sets contains a copy of itself in an obvious way.
The secret to Julia sets is that they aren’t more complicated — they just have a different kind of self-similarity. Instead of containing themselves, Julia sets cover themselves. In particular, each of the three Julia sets above has an order-two symmetry around its center point, and the quotient of the Julia set by this symmetry is homeomorphic to the original Julia set.
Roughly speaking, if the Sierpinski gasket is “self-similar” (meaning that it contains itself), then a Julia set is “co-self-similar” (meaning that it covers itself). This leads us to a general investigation of co-self-similar graphs.
Graphs that Cover Themselves
The simplest graph that covers itself is the circle:

In particular, the angle-doubling map winds the circle around itself twice, forming a double cover.
Things become complicated, though if we wish to add anything to the circle. Suppose, for example, that we wanted to add an edge jutting out of the circle from the point :

The self-covering-map on the circle cannot be extended to include this edge. In particular, the point is in the preimage of
, so it would also need to have an edge sticking out of it:

Now that we’ve added an edge at , we’re going to have to add edges at
and
if we want to maintain the cover. Eventually we will arrive at a circle with one edge attached to each dyadic fraction:
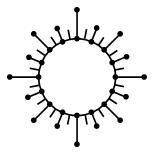
Though this has ceased to be a “graph” in the strictest sense, we have arrived at a topological space that covers itself. This is a very basic example of a co-self-similar fractal.
Note that each stage of this construction is actually a cover of the previous stage:
Indeed, there is a nice commutative diagram:
Here the ‘s are the stages in the construction, the horizontal arrows are covering maps, and the vertical arrows are inclusions.
A More Interesting Example
Let’s look at something more interesting. Consider the following graph:

This graph consists of two loops at a single vertex, and we have already specified a partial self-covering: the red loop maps to the blue loop, and the blue loop maps twice around the red loop.
This isn’t currently a covering map — the blue loop needs a second preimage:

That fixes the problem with the blue loop, but now the red loop on the right needs a pair of preimages:

Both of the new green loops map to the red loop on the right. (Do you see how this graph is a double cover of the previous one? As we double the angles on the blue loop, the left half of this diagram moves counterclockwise around the bottom and then joins with the right half.)
In the next step we add preimages for the pair of greens:

Here the orange loops map to the green loop on the right, and the pink loops map to the green loop on the left.
Let’s skip ahead three stages:
By this point, the fractal is really starting to take shape. The number of branches coming off of the blue loop (and indeed every loop) will continue to increase. In the limit, there will be one circle attached to the blue loop for each dyadic rational.
This example is interesting because it is a Julia set. These graphs are converging to the basilica:
The basilica is the Julia set associated to the map . The central loop surrounds the point 0, while the loop immediately to the left of center surrounds -1. The map
switches these two points, and maps the basilica to itself as a double cover.
Next time I’ll explain exactly what a Julia set is and why they self-cover, and I’ll try to make the connection between the dynamics and combinatorics more definite.



July 23, 2007 at 5:26 am |
Fascinating post! But what about the Mandelbrot set? Is it self-similar or co-self-similar?
July 24, 2007 at 3:52 pm |
The Mandelbrot set is nether self-similar nor co-self-similar in any simple way. It contains many approximate copies of itself (e.g., try zooming in on c = 1.75 , c=1.475, or c=0.16+1.03i using this applet), but each of these is subtly different from the original. It also has a complicated network of branching strands connecting the various copies whose structure is not well-understood. Take a look at the zoomed-in pictures on the Wikipedia page to get a sense of the awesome complexity.
Part of the point that I’m making is that Julia sets aren’t like the Madelbrot set. Someone without a computer would have a very hard time understanding the structure of the Madelbrot set, but Julia sets can very reasonably be drawn by hand.
October 31, 2008 at 8:20 pm |
Hello,
Has anyone tried to marry fractal math with stochastic processes?
thanks, richardhot
October 31, 2008 at 11:40 pm |
Has anyone tried to marry fractal math with stochastic processes?
Only just about everybody.
May 11, 2011 at 1:14 pm |
Hi.
Thx for intresting article.
Here is similar model for Mandelbrot set :
http://commons.wikimedia.org/wiki/File:Circle_7_4.svg
Regards
December 31, 2017 at 2:30 pm |
See also : https://commons.wikimedia.org/wiki/File:Shrub_model_of_Mandelbrot_set_60_10_labelled.png
May 31, 2019 at 1:56 pm |
these are important example observed prof dr mircea orasanu and
prof drd horia orasanu followed JULIA