I tend to think of homotopy theory a little bit like ‘The One That Got Away’ from mathematics as a whole. Its full of wistful fantasies about how awesome it would have been if things could only have worked out. Imagine if homotopy groups of spaces and homotopy classes of maps were as easy to compute as homology groups… we’d be teaching undergrads about Postnikov towers and topology might very well end up a subset of group theory.
Instead, homotopy theory is a hopeless, incalculable mess in all but the trivial cases… that bitch. The canonical example here is the Toda’s Table of the Homotopy Groups of Spheres. That’s right, even the simplest imaginable case – homotopy classes of maps between spheres – is a wildly unpredictable mess with only a handful of a structure theorems.
So homology and cohomology theories rule the day; not as powerful as homotopy groups, but infinitely more tractable. However, recently I’ve become somewhat enamored of a weaker form of homotopy which is just weak enough where you can actually say things: Rational Homotopy Theory. The general idea is to simply ignore any information coming from torsion homotopy groups. After all, all the hideousness in Toda’s table is finite groups; we know the infinite homotopy groups, and they represent reasonably interesting phenomena.
The main upshot of this is that all the information of a space (up to rational homotopy) can be packaged in a differential graded algebra. Rational homotopy equivalence becomes quasi-isomorphisms, and so the question of whether two spaces are rational homotopic is very reasonable. With some mild restrictions, it can be shown that spaces up to rational homotopy are the same as DGAs up to quasi-isomorphism. This opens the door for recasting much of topology as purely algebraic constructions.
For the sake of concreteness, whenever I say ‘space’ in this post, I mean connected CW complex.
We want to think about passing from the category of spaces to the homotopy category of spaces, but we would like to be as lazy as possible. We could identify any pair of maps which are homotopic, but it turns out we can get away with only identifying pairs of maps which are homotopic and are homotopy equivalences. To see this, notice that any homotopic maps factor through the maps
, and
and
are homotopic and homotopy equivalences, so
and
also get identified.
This may seem like a rather silly point to make, but the advantage is that the latter class of maps is easier to characterize algebraically.
Whitehead’s Theorem. A map
between spaces
and
is a homotopy equivalence if it induces an isomorphism on all homotopy groups. Furthermore, two such maps are homotopic if and only if they induce the same isomorphism.
Hence, to form the homotopy category, we can identify maps which induce the same isomorphism on homotopy groups. This is usually done by adding arrows to the category which are formal inverses to such classes of maps.
This leads naturally to the definition of rational homotopy. Given a space , we can throw away all the torsion information in
by tensoring with
; ie, looking at the rational homotopy group
. Inspired by Whitehead’s theorem, we say a map is a rational homotopy equivalence if it induces an isomorphism on all rational homotopy groups, and two such maps are rationally homotopic if they induce the same isomorphism. Thus, we can form the rational homotopy category by adding formal inverses to rational homotopy equivalences.
This is a coarser equivalence relation on spaces than you might think. To get a sense for what is going on here, think about any finite-sheeted covering map . This induces an isomorphism on all
, and a surjection on
with finite order kernel. Therefore, it is an isomorphism on all rational homotopy groups and hence a rational homotopy equivalence.
So rational homotopy is blind to quotienting by the free action of a finite group. This may seem weird, but in some ways it is desirable. Take, for instance, the study of hyperbolic Riemann surfaces. By the Riemann mapping theorem, these are all quotients of the hyperbolic disc by some subgroup of (a Fuchsian group). A useful relationship between two Fuchsian groups is that of commensurablity, that is, having intersection which is cofinite in each group. By the same argument as the previous paragraph, two Riemann surfaces with commensurable Fuchsian groups are rational homotopy equivalent (and the converse is also true).
Ok, so this is all well and good, except that homotopy groups are hard to calculate, and we don’t really know how much easier will be to compute. Thankfully, there is a theorem of Whitehead and Serre’s which allows us to avoid this entirely:
Theorem (Whitehead-Serre). A map
induces an isomorphism on all rational homotopy groups (ie, is a rational homotopy equivalence) if and only if the map induced on all rational cohomology groups
is an isomorphism.
Therefore, we can go back and redefine the rational homotopy category by inverting morphisms which induce an isomorphism on all rational cohomology groups.
Here’s where the algebra comes in. To any space we can assign its cochain complex
. This determines a functor from the category of spaces to the category of differential graded algebras; specifically DGAs which are commutative and have no negative-degree terms. Let’s call these DGAs topological, and we can endow them with an equivalence relation by inverting maps which induce isomorphisms on cohomology (quasi-isomorphisms).
Then the rational homotopy category of spaces maps into the category of topological DGAs modulo quasi-isomorphism. What is even better is that if we restrict to simply connected, finite dimensional spaces , and topological DGAs which are finite dimensional in each degree and have zero first cohomology, then this functor is an equivalence of categories.
This allows us to abandon spaces entirely and work with DGAs. I find this personally very satisfying, since I already know several circumstances where it is useful to think of DGAs as almost like spaces, and this theorem lets me know exactly what is lost when thinking like this (its the information inaccessible to rational homotopy theory).
This also transitions into one of the most fun aspects of math (at least for me personally), which is taking an equivalence and seeing what natural constructions on one side look like on the other side. Topology is full of natural constructions like various topological products, suspensions, loop spaces, classifying spaces, fiber bundles, etc… Each of these becomes an interesting construction on DGAs which might otherwise seem bizarre and unmotivated. If the mood strikes me, I might write a follow-up post to these outlining some of these constructions.
April 27, 2008 at 6:24 pm |
Greg,
A finite sheeted covering induces an injection on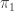 with finite cokernel. There’s no reason for this to be an isomorphism after tensoring with
with finite cokernel. There’s no reason for this to be an isomorphism after tensoring with 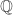 . In fact, if F is a free group then for every proper subgroup of finite index, the induced map on abelianizations has infinite kernel, by Nielsen-Schreier.
. In fact, if F is a free group then for every proper subgroup of finite index, the induced map on abelianizations has infinite kernel, by Nielsen-Schreier.
April 27, 2008 at 6:45 pm |
Is there a natural candidate for “???” in the following:
integer cohomology —> rational cohomology = rational K-theory rational homotopy groups <— ???
I’ve long been convinced of the idea that integer cohomology is a mistake, whose good properties should be attributed to integer K-theory, the correct thing to calculate. So I wonder if rational homotopy theory has some other integral structure that’s better than ordinary homotopy.
April 27, 2008 at 11:45 pm |
Hmm…interesting. I’ve always found homotopy dreadful, which is funny since I love algebraic topology and it is the first thing everyone learns. I always found it to be so patched together, sort of like “the standard model” in physics. Very rough and inelegant. Cohomology is much nicer. I may have to look into this rational homotopy. It looks much better.
April 28, 2008 at 1:46 am |
Ben, thanks for the heads up. That was a pretty boneheaded mistake on my part, and now I don’t have a good example of a general class of rational homotopy equivalences. The annoying part is that alot of finite-sheeted covers are still rational homotopy equivalences.
April 28, 2008 at 7:12 am |
If the mood strikes me, I might write a follow-up post to these outlining some of these constructions.
Please, oh please do!!
April 28, 2008 at 9:11 am |
Hi Greg – nice post! rational homotopy theory is indeed da bomb.
I’ll resist going on a full scale rant but let me just say I think
saying homotopy groups are a wild mess and failure
is equivalent to saying Galois theory is a failure since
the absolute Galois group of Q is so far from understood, or that
the integers are a catastrophe since the zeros of the Riemann
zeta are complicated, or that elliptic curves are a disaster since
we know hardly know the ranks of elliptic curves over Q, etc.
It is not that homotopy theory was to be a part of group theory,
but as Quillen started to show the converse is true – currently
a big swath of algebraic geometry can be seen as a special
easy case of homotopy theory, but with great insight
to be gained from the broader perspective. In fact it is apparent
that algebraic geometers largely ignored homotopy theory
only at great cost and that is beginning to change.
Homotopy theory is an incredibly rich beautiful subject with
many overarching themes, large scale patterns, deep
phenomena related to the most beautiful parts of number
theory and geometry etc. It certainly has suffered from very
bad salesmanship for a long time but Hopkins, Madsen, Lurie
and others are changing that hopefully.
April 28, 2008 at 9:14 am |
One more thing – there’s an analog of rational homotopy theory
over the integers as well, due to Mike Mandell — the integral
homotopy of spaces is captured by a generalization
of rational dgas, which are known as E_infty algebras –
roughly speaking chain complexes with a homotopy-very-very-commutative
multiplication (the functor from spaces to E_infty algebras
is taking integral cochains – the claim is these
with their cup product structure actually capture homotopy types!)
April 28, 2008 at 11:56 pm |
Eek, some of the stuff I put in was eaten as being HTML for “ignore this comment”. Too bad there’s no preview function here!
Is there a natural candidate for “???” in the following:
integer cohomology TO rational cohomology = rational K-theory FROM integer K-theory
integer homotopy groups TO rational homotopy groups FROM ???
April 29, 2008 at 1:40 am |
David – I started looking in to this stuff after your comment on topological Kozsul duality, which I think I am a day or two away from understanding. I’ll concede the point that homotopy is not the wasted effort I made it out to be; though I won’t apologize for trying to stir up trouble.
As far as algebras go, are these some kind of algebra object in a model category? I’ve seen Jacob Lurie talk about them, but I’ve never really figured out how to think about them. I mean, a dga up to q-ism is the same as its homology ring plus some information about how it fits together (an
algebras go, are these some kind of algebra object in a model category? I’ve seen Jacob Lurie talk about them, but I’ve never really figured out how to think about them. I mean, a dga up to q-ism is the same as its homology ring plus some information about how it fits together (an  structure). Will these
structure). Will these  algebras be something similar, like the homotopy groups
algebras be something similar, like the homotopy groups  together with some nebulous data as to how they fit together?
together with some nebulous data as to how they fit together?
(P.S. Sorry you got caught in the spam filter. It should know you now and not catch you again)
Allen – David’s suggestion might be what you are looking for, but I wouldn’t be the one to ask. Can you be any more specific about what kind of nicer integral struture you were looking for? I don’t have any candidates in might, but it’d be interesting to hear what you were hoping might happen.
April 29, 2008 at 5:23 am |
I think this sentence needs fixing:
“So homology and cohomology theories rule the day; not as powerful as homology groups, but infinitely more tractable.”
Homotopy theory, like any truly interesting subject in mathematics, will never be fully nailed down. Everything you can completely understand loses interest – except as a tool for understanding harder things.
April 30, 2008 at 12:38 am |
Can you be any more specific about what kind of nicer integral struture you were looking for?
Not off the top of my head.
I can explain a couple of ways in which integer K-theory is strictly nicer than integer cohomology, but I can’t turn them into desiderata for a different integral structure inside rational homotopy.
#1 is that there’s a spectral sequence computing K-theory from cohomology, with which one can see that the size of the torsion group (if it’s finite) in cohomology bounds that in K-theory.
#2 is that on flag manifolds G/B, there is an obvious list of line bundles with which to try to generate H or K. They do in fact generate the ring K, hence K @ Q, hence their (first) Chern classes generate H @ Q. Now, H itself is torsion-free, so you might hope that they generate H. No, only for G = GL_n is this true.
Perhaps to give an answer to your question, I should first understand the rational homotopy of flag manifolds, then decide what I want the integer part to be.
May 2, 2008 at 9:49 pm |
Do you feel as badly (worse?) about the Chow ring as you do about integral cohomology? Relatedly, is the Chow ring of a flag variety the same as its integral cohomology ring?
May 7, 2008 at 3:04 pm |
is the Chow ring of a flag variety the same as its integral cohomology ring?
I think so; any cycle is equivalent to a B-invariant one, hence to a sum of Schubert cycles. So that handles the groups. Then via Kleiman-Bertini, the product of cycles is going to work the same thought of topologically or intersection-theoretically.
April 17, 2010 at 7:30 am |
For the Whitehead theorem, i can give the following example,(IRP^m)x(S^n) and (S^m)x(IRP^n) have the same homotopy groups but not the same homology groups.
August 29, 2010 at 10:30 pm |
A nice example of a rational equivalence arises whenever a finite group G acts on a simply connected space X trivially on homology: the map X –> X/G is a rational equivalence, aside from the fundamental group of the quotient being wrong. There are learned ways around this, but one simple way is to introduce fixed points. If the action of G fixes a point, then the quotient will be simply connected, and then the quotient map is a rational equivalence.
Another good general example are Kahler manifolds with isomoprhic cohomology rings (thanks to Deligne, Griffiths, Morgan, and Sullivan). Or spaces whose cohomology is a polynomial algebra tensor and exterior algebra (thanks to Borel and Serre, essentially).
June 1, 2012 at 9:31 am |
Why include sexist insults in articles about math? No, I don’t wish to read an answer. Just do me a favor and think about how some people might feel when they read an article about rational homotopy theory and then realize that they stumbled into a fraternity party unknowingly.
June 22, 2012 at 4:08 pm |
A counterexample to the second part of your “Whitehead’s theorem” (that two maps are homotopic if they induce the same isomorphism of homotopy groups).
Let $(G,e)$ be an H-space, that is, there is a continuous map (“multiplication”) $G\times G\to G$ such that $eg=ge=g$ for all $g\in G$.
Let $(B,b_0)$ be a pointed space and $f\colon(B,b_0)\to(G,e)$ be a map that induces a trivial homomorphism of homotopy groups and a non-trivial homomorphism of rational homology groups.
Then the map $B\times G\to B\times G$, $(b,g)\mapsto(b,f(b)g)$, induces the identity endomorphism of homotopy groups and a non-identity endomorphism of rational homology groups.
Thus this is a couterexample.
One may take $G=S^7$, the unit octonions, and $B=S^3\times S^4$, then let $f\colon B\to G$ be any map with non-zero Brouwer degree.
November 27, 2013 at 4:38 pm |
Is the Whitehead Serre theorem really true in the form you quoted?
In the sources available for me there is a condition that the spaces must be simply connected.
August 3, 2014 at 4:24 pm |
Let $X$ be a finite simply connected CW complex. It is true that either $H_*(\Omega X; \mathbb{Z})$ has $p$ torsion for all but finitly many primes $p$ or else that $H_*(\Omega X;\mathbb{Z})$ has $p$ torsion for only finitely primes $p$? The question has a positive answer for rationally elliptic spaces $X$ since C.McGibbon and C.Wilkerson “Loop space of finite complexes at large primes”.Proc.Amer.Math.Soc.96 (1986), 698-702shows that then $H_*(\Omega X; \mathbb{Z})$ has $p-$torsion for only finitely many primes, so what do we can say about $H_*(\Omega X; \mathbb{Q}_p)$ and if $X$ is an $k-$ unordered configuration space? I think that there is a condition on degree of homology (cohomology) classes and on $k.$
December 18, 2017 at 11:40 pm |
Thanks for sharing your thoughts about w. Regards