I alluded in one of my very first posts here to a calculus class that I was teaching using the ring ![\mathbb{R}[dx]/(dx^2 = 0)](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BR%7D%5Bdx%5D%2F%28dx%5E2+%3D+0%29&bg=ffffff&fg=333333&s=0&c=20201002)
. The class was a six-week, 5-day-per-week intensive course covering the usual material of a college Calculus I course. I’ve been promising Greg and Jim that I’d write up some of my experiences with the course. I think I have had enough time to process the experience — let’s talk non-nonstandard calculus.
Maybe a word about the name before we begin: I think that a lot of my philosophy on mathematics came from taking several analysis classes at Smith College from logician Jim Henle. I learned nonstandard analysis from him one summer, but also learned what he called “non-nonstandard analysis”. The idea was to get infinitesimals into calculus without the big ultrafilter-style logic machinery of standard nonstandard analysis. I’d like to say more about this version of non-nonstandard analysis sometime in the future, but not just this moment. But the main idea is this: we want infinitesimals, but we don’t want to bring in the heavy machinery if we can avoid it. The (serious) tradeoff is that we lose the transfer principal when we use non-nonstandard analysis.
Now, a bit more about the class I taught. Most students had not seen much beyond precalculus. Maybe they had been told how to formally take derivatives of polynomials, but not much more. So I had a fantastically clean slate to work with. This may have seriously affected the outcome of the class.
In the first serious lecture, I introduced 
as a positive number so small that 
. They thought this was a little funny, but came around to it after I drew an analogy to 
and 
: even if they had philosophical objections to thinking about or as “numbers”, their recent experience with complex numbers in high school put them in a good place for accepting as a useful formal symbol, if not an honest-to-goodness number.We could then quickly move on to computing the derivative of some elementary functions like 
:
I also pointed out that computers are using a number system which is closer to this than it is to 
: since floating point processors have finite precision there is a smallest positive denormal. It must square to zero. So if you are judging mathematical truth by “is relevant to things I know in the real world”, it seems that nilsquare infinitesimals aren’t such a strange idea.
On the second day, I gave them a few useful tidbits: as an axiom, I said 
. Then by looking at a right triangle of height , we decided that 
and 
. From here, it is easy to compute derivatives of relatively complex functions by hand. By the end of the third day, there were homework problems (generally solved correctly) like “use the definition of the derivative to find the derivative of 
”:
so the derivative is 
.
By asking them to compute the derivative of things like 
or 
by hand, they rapidly re-learned (and remembered!) the angle-sum formulas for sine and cosine and the algebraic rules involving exponents. I never allowed formula sheets or calculators or anything like that in the class or on the tests — the kids were genuinely remembering the formulas and the derivations. Even the weaker students at the end of the course could all compute the derivative of as a routine computation:
but even better, they remembered 
or 
because these manipulations had become common to them. They used them every day in nearly every problem, and they remembered. No formula sheet hell involved.
When a number like 
appeared in the denominator, the students quickly figured out that they could multiply on the top and bottom by 
to “realify” the denominator. I was surprised that they saw this trick so quickly, until I realized that they had been doing the exact same thing with complex numbers for several years already. The derivative of 
, with no more than two steps left out:
On the final, I asked them to compute the derivatives of 
, 
, and 
from the definition. Almost uniformly, the students could create correct computations of the derivative. The next question on the final was “prove the quotient rule”. Nearly everybody in the class, even the C-students, did this derivation properly. They were not told beforehand that anything like this would be on the test.
Another thing which they were fairly good at was using differentials, since the differential was not some mysterious formal symbol to them but an actual infinitessimal value. From this perspective, it is easy to see how to use differentials to get good approximations. This also made it as easy to work with implicit differentiation as with explicit differentiation, which it turn makes computations of related rates much cleaner than usual. From my perspective, it also makes the usual geometric ways of demonstrating the product rule or the fact that 
more rigorous: the area added really is just some lengths times the width of my chalk. By treating infinitesimals on the same footing as finite numbers, the approximation schemes of calculus become more intuitive. I think every mathematician has discovered this on their own, in their own private language. Why not make the language commensurable with the computations that we do?
I’ll write plenty more about the other topics of the course in the future, but this should give you some idea of what the class was like and why I felt that nilsquare infinitesimals were a productive way to teach calculus. We really didn’t use limits at all: they were all replaced with infinitesimals and approximation schemes. It is true that limits, infinitesimals and approximation schemes are all equivalent ideas, but I believe the latter two more closely model our internal, geometric understanding of calculus. So: what do you readers think?
This entry was posted on August 28, 2007 at 11:10 pm and is filed under Basic Grad Student, High School, Matt, Undergraduate. You can follow any responses to this entry through the RSS 2.0 feed.
You can leave a response, or trackback from your own site.
The Everything Seminar 
August 29, 2007 at 12:46 am |
Actually, it reminds me of something Louis Kauffman has on his door. It’s all of integral and differential calculus on two pages, and the only difference is he uses a lowercase delta instead of dx.
My qualm here is that you manage to completely bypass limits. What effects do you think this will have when the students hit series, if they ever do?
December 19, 2016 at 3:38 pm |
Please see my comment, in which I described how to use matrices and a “lexicographic” ordering to bring back into this the “analysis” aspect that makes it so you should be able to connect all of this with limits fairly effortlessly…
August 29, 2007 at 4:15 am |
Very nice. I would be really interested in what you think the disadvantages of this approach are. There must be many, as some sort of balance to the many advantages. Probably the best way to think of them is to teach a course and see what happens.
August 29, 2007 at 5:42 am |
I am very intrigued by the nonstandard approach to calculus. Could you point us to some good introductory books/lecture notes?
August 29, 2007 at 6:23 am |
Is this just a rephrasing of automatic differentiation with dual numbers? It seems that your students may run into trouble later because they don’t understand enough abstract algebra to know what’s going on, and may just resort to manipulating symbols without any real understanding when things get tough.
I’ve never been much of a calculus guy (barely learned enough to get through diffeq and real analysis), so please excuse any ignorance on my part.
Thanks
August 29, 2007 at 6:47 am |
And that’s not what they do now?
December 19, 2016 at 3:39 pm |
You’re right, I think…
August 29, 2007 at 7:21 am |
So does non-nonstandard analysis have anything to say about the integral? It seems nice for differentiation, but I don’t immediately see how to use the dual number approach to integrate.
December 19, 2016 at 3:41 pm |
The nonstandard analysis of Robinson certainly explains integrals using infinitesimals. In smooth analysis, it seems to me that one only describe differentiation, and then anti-differentiation, and you are done, but with a weakening of the connection with geometry (integrals as area).
August 29, 2007 at 9:52 am |
This looks very nice. I’ve been curious for a while whether I could teach calculus using big O notation as the fundamental object instead of limits, and this looks like a similar but easier approach. Question — what do you plan to do when you get to Taylor series? When I do calculus computations, that’s when I start really hauling out the big O’s. (For example, try computing the first three nonzero terms of the Taylor series for sqrt(cos(x)) by repeated differentiation, and then do it again by expanding (1-x^2/2+x^4/24+O(x^6))^{1/2} by the binomial theorem.)
August 29, 2007 at 10:51 am |
This is indeed a nice way to do differentiation, but it may run into some trouble once one leaves the category of smooth or analytic functions. For instance: is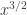
differentiable at x=0? What about 
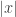? etc. More generally, it is hard to detect non-differentiability in this setting. (This is the usual phenomenon in algebra that it is easy to prove two things are equal, but difficult to prove that two things are unequal. Analysis, of course, has the opposite problem 🙂 .)
Also, one may encounter some difficulty with second derivatives. One wants to assert the formula
, but you can’t do that within the ring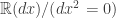 
– division by zero error! For similar reasons, it is a little tricky to justify any Taylor expansion beyond first order.
Finally, it’s not particularly easy to show
in this framework, which will lead to some problems when one gets to the indefinite integral. Nevertheless, one can at least get the fundamental theorems of calculus by postulating the existence of a definite integral operation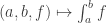 
which obeys some reasonable axioms (linearity, concatenation, translation-invariance, and most importantly that 
).
Things also get rather interesting in several variable calculus: what ring would you use, for instance, to prove Clairaut’s theorem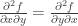
? (and how do you deal with the fact that this theorem can in fact fail for certain twice differentiable functions?). And Stokes theorem is going to be particularly challenging without using much more of the machinery of infinitesimals than just 
.
In short, it is a nice way to get students quickly started on single-variable differential calculus, but one should also be prepared to move beyond this approach when one wants to tackle the rest of the calculus.
December 19, 2016 at 3:54 pm |
Terence,
Your concern about the formula for second derivatives may be assuaged by using nil-cubed infinitesimals and a relation like the following (I’ll write it in LaTeX, because I haven’t used WordPress enough to know how you embedded your nice pictures of formulae):
dx\approx 0
\Rightarrow f(x)\approx 2f(x+dx)-f(x+2dx)+f^{\prime\prime}(x)dx^2.
The nil-square infinitesimals will trivially satisfy this (where the notation \approx means “infinitesimally close”), but the nil-cubed ones will remain in the equation, helping with the use of the second derivative.
Of course, for higher-order approximations, you need higher-order nil-potency, and that begins to be a bit shaky ground for low level students. In a post later (unfortunately labeled as “Anonymous”), I laid out the outline of an approach for this using matrix algebra, and extending the ordering of the real number ring to a ring of matrices.
August 29, 2007 at 10:58 am |
p.s. This approach is excellent for introducing the concept of a tangent bundle, and interpreting the derivative of a map between manifolds as a linear map between two tangent bundles. Indeed, one can argue that this approach is basically the algebraic way of viewing R as a manifold. This also clarifies a bit the difficulties mentioned above; second derivatives on manifolds are indeed a real pain, one needs the machinery of connections. Also, now that one has some non-trivial global cohomology, it’s clearer as to why things like Stokes’ theorem are not going to be trivial.
August 29, 2007 at 11:25 am |
Re: John’s question about bypassing limits. As we got further into the course, and the student’s got more used to approximation schemes (differentials, Newton’s method, Riemann sums for area and Riemann sums for solving a differential equation), I think that their ability to think about limits developed on its own. We talked about limits long enough to discuss L’Hospital’s rule near the end of the course. During this class, we developed a translation dictionary on the board between limits and infinitesimals. Those who had seen the derivative defined before had a “oh, I see where that h thing came from” moment. It was heart-warming. I have trouble believing that there is enough content in the idea of “limit” that a decent students couldn’t pick it up rapidly when they begin to deal with series in Calc 2. This use of “limit” is just “this sequence of approximations is as good as you would like”, after all.
I am planning on emailing the students after another several weeks have passed to see how they are doing in the next calculus course. I think this will be the real test of the idea, and I will be sure to pass the results along.
August 29, 2007 at 11:33 am |
Shaneal, you are right that this is the same idea that is exploited with automatic differentiation. But I don’t think the students saw it as purely formal — I talked about infinitesimals on equal footing with real numbers, we drew chalk-sized infinitesimal things in our diagrams, and most importantly the students began to correctly use the language: “A and B are infinitesimally close” and so forth.
I’m not sure, but I suspect that by using honest equations rather than limits in (for example) the definition of the derivative, the students are more inclined to understand what is going on. The definition of the derivative via dx is, after all, just an equation; the one with limits carries an implicit “for all / there exists” in front of it. The more
alterations, the harder it is to understand the underlying idea.
August 29, 2007 at 11:40 am |
p.p.s. There is another slight issue, which is to decide as to whether dx is “positive”, “negative”, or “neither” (the latter is what happens of course with i = sqrt(-1)). This becomes relevant when one wants to show that a function has derivative zero at local extrema. One can work around this issue by having both positive and negative infinitesimals (and thus deal with right and left derivatives), but this approach does not extend well to several variables.
It’s also worth noting that Ito calculus is traditionally presented using this algebraic infinitesimal approach, by adjoining an additional relation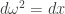
.
One final advantage (or disadvantage, depending on your point of view) is that this approach does not really use the structure of the reals and so also applies over arbitrary fields. As such it is highly compatible with algebraic geometry, schemes, etc. (This also explains why it is not so terribly compatible with the definite integral, or the detection of local extrema.)
December 19, 2016 at 3:58 pm |
The approach using matrices and a “lexicographic” ordering helps with this: One gets a natural “unit infinitesimal”, and the rest of the infinitesimals are real multiples of it, and that unit infinitesimal is positive, so that negative multiples of it are negative infinitesimals and positive multiples of the unit infinitesimal are positive infinitesimals.
August 29, 2007 at 11:42 am |
This approach seems to me problematic for three distinct reasons.
First, there is little benefit. Actually computing derivatives can be taught in half-a-day with a few formulas. You need only the product, quotient, chain, and power rules, as well as a couple of memorized formulas (derivatives of exp, ln, cos and sin). Since this is not a problem, there is no reason to modify the way to teach the simplest part of calculus. The hard parts of calculus are limits, series, integrals, extrema, n-dimensionality, discontinuities, differential equations, and word problems. Derivative computing is just not hard for anyone who will be able to master the rest of calculus (those for whom it is hard won’t learn calculus anyway).
Second, the approach does not prepare students to read and understand works written by the remainder of the mathematics, physics and engineering community.
Third and most important, the approach misconstrues the purpose of teaching calculus. This purpose is not solely to teach students to manipulate derivatives. Instead, it is to teach them to understand concepts of rigor, proof and meaning. Calculus is the course where teachers should not lie to students about the true meaning of what they do. This method, even it works to the extent of being useful mnemonically, shortchanges students because they are deceived as to why it works. I don’t see that students have any real understanding of derivatives using this method, even if they can compute them.
That said, the differential notation is nonetheless powerful and useful in its own right, but should only be introduced after students have understood the limit formalism. Thus, I would introduce limits, and them spend some time on the differential notation.
August 29, 2007 at 11:51 am |
Terry: one sharp kid pointed out exactly your point about second derivatives in one of the first classes: “but don’t we write
for second derivatives?” The problem is really that when you need to do things like take second derivatives, you need to keep track of two potentially incommensurate infinitesimals at once. Some of our early posts on the blog mentioned how even if dx and dy are nilsquare, unless you know that dy/dx is finite then the sum (dx + dy) is only nilcube. (dx + dy) becomes nilsquare again if you propose that dx dy = -dy dx, and suddenly it seems that we are about to start a conversation on 
with freshman. This is certainly a big drawback to the approach: infinitesimals on different orders of magnitude are too messy, so you have to stick close to situations involving only one infinitesimal scale. For a calculus 1 course, this is not so strict a requirement. For a calculus 3 or analysis course, it is probably not worth the effort.
You can, of course, use nilcube, nil(4th), … infinitesimals to compute second and third derivatives directly, using exactly the formula that you have written. This is also one way to tackle Taylor series in the same spirit.
Detecting non-differentiability is not so bad after all. In fact, it is remarkably easy to do on the class of “high school functions”. On one test, they had to show that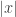
was continuous but not differentiable at 
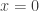. To see continuity, you only need to note that the three (and only three!) numbers 
, 
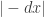and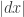 
are infinitesimally close. To see that the derivative doesn’t exist, you only need to compute the left and the right derivatives (using 
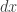and 
) to find out if they agree. I want to write much more about this aspect of the class soon, because it was one of the most philosophically confusing aspects of the course to me.
Your description of how we have to approach integration is pretty dead-on. More on that in a future installment 😉
August 29, 2007 at 12:30 pm |
fjfjj: Your criticisms are reasonable, but I think misguided. I overemphasized computing derivatives from first principles in this post, but the computation of derivatives was of course only a very small portion of the class. I will be writing about the other aspects of the class in the near future. I believe that for most students, the hard part of calculus is modeling: they do not know how to translate ideas about the world to equations which they can manipulate, and they don’t know how to take an equation and create a mental model of what it represents. This is manifested in how strongly they avoid word problems of the optimization or related rates types, even though these problems are almost trivial once an actual equation has been written down.
The idea of this course was not really “look at this funny trick for computing derivatives” but rather “can I teach calculus so that the symbolic methods we use more closely model the intuitive ones”? It is not clear that these students were better than my previous limit-ed ones at word problems, but they certainly weren’t any worse.
As for your second reason, I simply can’t agree. Even while I was still teaching the class, one student commented that her physics instructor was impressed that she was learning calculus “the right way” [with infinitesimals]. In his work, the infinitesimal displacements were real quantities to be manipulated.
As for your third point, I don’t understand how it deceives the students. It works for the exact same reason limits or O-notation or nonstandard analysis any other formulation of calculus works — it is a good model of the language of calculus. In at least this one case, the students came away with a better understanding of derivatives than usual. They can understand the derivative directly, getting their hands right on it through computation or seeing the tangent line between two infinitesimally close points. I’d like to better understand why this approach seems deceitful to you, since I have received similar reactions from several other people.
August 31, 2007 at 9:56 am |
[…] Non-nonstandard Calculus, I […]
September 3, 2007 at 2:09 pm |
As a physics major with an undergrad math focus, I had a chip on my shoulder about infinitesimals versus limits. In physics classes, we talked about infinitesimal quantities all the time, but I always mentally translated them into limits, believing that this was the only correct way to think about it. I ran into calculational difficulties with this mental model in grad school, finding that my peers could solve problems I couldn’t even get my head around, and, after some discussion, we found that it was because they truly believed in infinitesimals. When I decided to admit them as a useful fiction, statistical mechanics got a lot easier. It would have been great to have seen both tools, and to have known the limitations of each (though that can be hard to teach to students who are looking for The Right Way to Think).
Thanks for the great post, Matt! By the way, what kinds of students were you teaching: engineering, physics, or math majors? Were they honors students or general?
September 10, 2007 at 1:53 pm |
Cos(dx/2) = 1;
Sin(dx/2) = dx/2;
Sin^2(dx) = dx^2=0;
from here:
0 = Sin^2(dx) = 2*Sin(dx/2)*Cos(dx/2) = 2 * dx/2 * 1 = dx > 0
0>0, congratulations.
June 18, 2011 at 1:03 pm |
sin(dx/2) = Sq((1-cosdx)/2) = 0 not dx/2
June 30, 2011 at 11:41 am
The correction above which negates the Sept 10 conclusion of “anonymous” was actually done by zenrin, not the original “anonymous.”
September 10, 2007 at 6:01 pm |
Is “Anonymous” somehow managing to confuse
with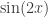 
?
September 27, 2007 at 1:31 am |
dx is a zero-divisor in the ring R[dx]/(dx^2), so if you invert it it becomes zero in the localization. How then can you algebraically justify dividing by dx?
September 27, 2007 at 8:18 am |
“How then can you algebraically justify dividing by dx?”
You don’t. You instead write f(x + dx) = f(x) + f'(x)dx for a unique scalar f'(x). This points to the difference between infinitesimal analysis using invertible infinitesimals (as in Robinson’s Nonstandard Analysis) and analysis which uses nilpotent infinitesimals (as in “Synthetic Differential Geometry”; see e.g. Mike Shulman’s paper here).
December 19, 2016 at 4:41 pm |
The same equation can be used in Robinson’s Nonstandard (Infinitesimal) Analysis, to define the derivative. One need not appeal to the invertibility of the nonzero infinitesimals, but their invertibility is available if you need or desire it.
October 1, 2007 at 5:46 am |
[…] Non-nonstandard Calculus, I « The Everything Seminar […]
January 13, 2008 at 9:02 am |
No, I didn’t get it mixed up – you got your . . . face . . . mixed up with . . . something stupid . . . I . . . . . . . .am a secret genius that the world has yet to discover! And I prove it by leaving obviously incorrect proofs misusing high school math on message boards without having the courage to leave my name hoping to score points from a safe distance that only I will keep track of on my mental scorecard (of course erasing this instance and most likely many others like it out of memory so as to maintain my delusion of superior intelligence . . . .(shhhhhhh!))
March 2, 2008 at 11:03 am |
Congratulations. You seem to have discovered the main features of smooth infinitesimal analysis (SIA). This is a version of analysis based on the repudiation of the general applicability of the law of excluded middle (LEM) and the principle of microstraightness of smooth functions. Nilsquare infinitesimals emerge naturally from these principles. SIA is entirely rigourous (its foundations are in Category theory) and it has at least four major advantages over Limit theory and non-standard analysis (NSA – which is just Limit theory in disguise). These are:
1. In SIA the differential calculus is reduced to simple algebra.
2. SIA does not lead to contradictions such as the Banach-Tarski
paradox as does Limit theory/NSA.
3. The method of microadditivity found in physical derivations is a
natural application of SIA but not of Limit theory/NSA.
4. The ‘taking the standard part’ fraud of NSA is unnecessary in SIA
because the infinitesimals cancel eachother out.
The best book on SIA is A Primer of Infinitesimal Analysis by J L Bell. Many of the criticisms of your approach given above are addressed in his book. I personally found it useful to compare Bell’s book with The Foundations of Mathematics by Stewart and Tall. In their book Stewart and Tall use the quest to explain calculus to justify the Completeness axiom and classical Real analysis – a justification which falls apart with SIA. They also use the Axiom of Choice in their coverage of Cardinal numbers; but this axiom also implies the LEM thereby disallowing nilsquare (that is, genuine) infinitesimals. Consequently, you can believe in infinite numbers or infinitesimals but not both, or at least not both at the same time. This may explain Cantor’s objection to infinitesimals! It is interesting to note that Fuzzy Logic also depends on the repudiation of the LEM. Calculus and Fuzzy Logic are perhaps the two branchs of mathematics which are the most useful in modelling reality. Perhaps Cardinals, ‘Real’ analysis, and the LEM should be banished to the fringes of philosophy.
December 20, 2016 at 2:43 pm |
Let us consider your “advantages”, one by one:
1. “In SIA the differential calculus is reduced to simple algebra.” Nonstandard Analysis does the same, but in fact, as has been pointed out, the question of whether this is an “advantage” depends upon whether one WANTS students to learn the limit concept or not. This is essentially a matter of taste, not a matter of rigor.
2. “SIA does not lead to contradictions such as the Banach-Tarski
paradox as does Limit theory/NSA.”
The Banach-Tarsi Paradox is merely a paradox. It is NOT a contradiction. The fact that some people call it a contradiction is not evidence that it is a contradiction. It seems counterintuitive, but ONLY UNTIL one realizes that the paradaoxical decomposition of the unit ball that allows recombination via rigid transformations into a ball of radius greater than one REQUIRES that the pieces into which it is decomposed be non-measurable. Thus there is no formal contradiction in this result at all.
3. “The method of microadditivity found in physical derivations is a
natural application of SIA but not of Limit theory/NSA.”
I am not familiar with “microadditivity” found in “physical derivations”, so I will look it up before completing my comment. First, though, I doubt that “physical derivations” makes sense. If I cannot find a definition of that term, I’m likely to reject this as a non-issue, based upon a vagueness in your terminology.
4. “The ‘taking the standard part’ fraud of NSA is unnecessary in SIA
because the infinitesimals cancel eachother out.”
I do not see how “the infinitesimals cancel each other out” in SIA. If all infinitesimals are real multiples of only one unit infinitesimal, then for any two infinitesimals dx and dy, the product dxdy is zero, I’ll grant you. However, if one’s SIA theory allows for nil cubed infinitesimals, then there will be some infinitesimals dx and other infinitesimals dy such that dxdy is nonzero. In this case, you need a “standard part map”, and referring to the standard part map in NSA as a “fraud” is disingenuous at best.
Your last paragraph contains several claims:
a. “The best book on SIA is A Primer of Infinitesimal Analysis by J L Bell.”
I’ve seen it and read some parts of it, but I’m not sure I could say it’s the best book on SIA. Can you list some others so that the interested reader can look them up and compare them themselves?
b. “Many of the criticisms of your approach given above are addressed in his book.”
Does John L. Bell use the term “fraud” in his book, in his discussion of NSA?
c. “I personally found it useful to compare Bell’s book with The Foundations of Mathematics by Stewart and Tall. In their book Stewart and Tall use the quest to explain calculus to justify the Completeness axiom and classical Real analysis – a justification which falls apart with SIA.”
I would have to look over the book by Stewart and Tall myself, but it seems to me that it is a matter of the historical record that the quest to explain or justify analysis (of which the common term “calculus” is used, in spite of the fact that that “calculus” to which the term is often applied is not the only caclulus) led to many of the discoveries of phenomena such as the Completeness Axiom, and many of the developments in classical Real Analysis. I’m not sure why this is a criticism…
d. “They also use the Axiom of Choice in their coverage of Cardinal numbers; but this axiom also implies the LEM thereby disallowing nilsquare (that is, genuine) infinitesimals.”
It is patently false that the Axiom of Choice disallows nil square infinitesimals. One can easily embed the ring of real numbers into a ring that includes nil square infinitesimals. Then you can use those nil square infinitesimals to your heart’s content, never running afoul of the Axiom of Choice or the Law of the Excluded Middle. Now, I have never before heard the claim that AC implies LEM, so please demonstrate, or give a reference. I want to see the proof that you claim exists. I expect that one reason I have never heard such a claim before is that it is rather strange. The LEM is a Law of one’s Logic System, and the Axiom of Choice is an Axiom of ZFC, in the language of Set Theory. One can use Intuitionistic Logic (or various other Logics without the LEM) and write down the axioms of ZFC. One can then study the Intuitionistic consequences of the Axiom of Choice.
e. “Consequently, you can believe in infinite numbers or infinitesimals but not both, or at least not both at the same time.”
Nonsense. NSA does exactly that, and the approach of NSA can be carried out in an Intuitionistic framework as well.
f. “This may explain Cantor’s objection to infinitesimals!”
It seems to me to be a bit precarious to claim to know what was going on in Cantor’s mind unless he told us what it was, so I won’t venture a detailed comment on this here. It is a matter of record, however, that people such as Bishop Berkeley objected to infinitesimals, and they objected to nil square infinitesimals, on the grounds that the theory of analysis using infinitesimals presented up until then was ACTUALLY inconsistent. If I had to guess, I would expect that Cantor was trying to avoid including blatant inconsistencies in his work.
g. “It is interesting to note that Fuzzy Logic also depends on the repudiation of the LEM.”
Fuzzy Logic can be presented as a special case of classical logic, and in fact, many presentations in an applied setting of Zadeh’s version of Fuzzy Logic (which came up late historically in Logic and Philosophy) are based upon very sophomoric views of Logic. One can observe in the Logic and Model Theory Community and Literature in the early twentieth century that “Fuzziness” of truth values was prevalent. The notion of a logic system whose truth values are taken in a Boolean Algebra appears, and plays a reasonably significant role, and you can see some of this in a text by John L. Bell and Alan Slomson called Models and Ultraproducts: An Introduction. An example of the “Boolean Fuzzification” of Logic is easily seen as a kind of overarching philosophy behind the development of notions like the Lindenbaum-Tarski Algebra, etc. Also in the early twentieth century, Quantum Logics were developed without the help of Lotfi Zadeh, and those are Logics whose truth values are taken in (often non-distributive) lattices, and so they often do not satisfy the LEM. Long before the twentieth century, philosophers discussed “modes”, and the resulting reasoning systems (often devised for argumentation in matters close to law and politics) are now called “Modal Logics”, and they form another family of “multi-valued logics”. “Fuzzy Logic”, depending upon what you mean by it, has been around for a long long time. By the way, it is known that using the interval [0,1] for your set of truth values, and the most common fuzzy interpretations of conjunction and disjunction and negation as in Lotfi Zadeh’s version of Fuzzy Logic is overkill, because three element logic will suffice. (See http://www.worldscientific.com/doi/abs/10.1142/S021848859700021)
h. “Calculus and Fuzzy Logic are perhaps the two branchs of mathematics which are the most useful in modelling reality.”
You’re leaving out combinatorics, probability, finite fields, finite groups, graphs, etc… Why? You might find it useful to look into the history of these subjects, which are not entirely bound up in “calculus”, and which use classical logic.
i. “Perhaps Cardinals, ‘Real’ analysis, and the LEM should be banished to the fringes of philosophy.”
No.
May 15, 2008 at 11:28 pm |
I recently wrote up some notes on Smooth Infinitesimal Analysis, the system for which the immediately preceding commenter is an aggressive advocate.
They’re at:
Click to access sia.pdf
The biggest contrast between Smooth Infinitesimal Analysis and Matt’s system (and non-standard analysis as well) is that while in both Matt’s system and non-standard analysis the object representing reals+infinitesimals is explicitly constructed and can be manipulated directly with the usual classical logic that mathematicians are used to, in Smooth Infinitesimal Analysis, the object representing reals+infinitesimals is presented axiomatically, and you must reason about it using intuitionistic logic in order to make the existence of infinitesimals consistent.
It sounds forbidding, but you can do a lot of pretty neat things with it.
May 23, 2008 at 6:00 pm |
I fear that some of the above comments may be slightly misleading. The objects that SIA deals with do not reside merely at the level of axiomatic description; they may be embodied in models which admit explicit constructions by taking categories of sheaves on appropriate sites. Externally speaking, one uses ordinary logic to describe these sites. It is of course true that the “internal logic” in such sheaf toposes is intuitionistic (meaning that lattices of subobjects of objects are not Boolean algebras; they are Heyting algebras), and it is in that sense that the inclination to manipulate the relevant objects directly as “smooth sets” must take intuitionistic logic into account.
May 23, 2008 at 10:36 pm |
You’re right, of course. I should have mentioned the models in my summary.
My reasoning for not doing so is that if one were to teach calculus via SIA, one would do so axiomatically and not via the models, just like we teach math majors to reason axiomatically in ZFC before we teach them (if we ever do) how to construct models of ZFC with set-theoretic forcing.
However, for people who are not learning calculus for the first time, learning how SIA works by going through the construction of the models may be the most enlightening way to do it. It could certainly help a classical mathematician who may be suspicious of or not fully understand intuitionistic logic to figure out what exactly is going on.
July 8, 2008 at 6:41 am |
Hi Folks, here is the “true” about the way to make pratical calculus, for Year when I’m at the University, the teacher tell me, “You cannoit semplify” the derivates, but in any kind of calculation they use the derivate as Fraction 😉
October 30, 2009 at 9:12 pm |
I have the book by Bell, but I do not like SIA because it denies the Law of the Excluded Middle without making it clear just when you can make a number both equal to, and not equal to, 0. On the other hand, those ultrafilters require the heavy logical machinery of the Axiom of Choice.
I prefer to use a proper subset of Robinson’s hyperreals (his R*) only requires the cofinite (Fréchet) filter on N. Call my subset R†, the set of ratios of real polynomials (the familiar “rational functions”) of the index variable, where two pairs of polynomials have the same ratio (belong to the same equivalence class) if the set of values of the index for which the ratios are not equal is finite.
This is the classic example of a non-Archimedean ordered set, and, if statements about polynomial ratios are considered true only the same conditions for equality hold, the transfer principle holds for all first-order statements. The proof requires only the properties of filters in general, and not the property of an ultrafilter that EVERY set of natural numbers or its complement has to be a member of the ultrafilter.
I am writing an appendix for Thompson’s _Calculus_made_Easy_ that uses my R† to justify the infinitesimals.
The great triumph of standard (real number) math is Weierstrass epsilon-delta definition of a limit, which tells one when one has found a limit (using only the real numbers), but leaves no clue as to how to find it.
In effect, nonstandard methods allow one to calculate beyond the infinite decimal precision of standard reals, and round off directly to the nearest standard real, the limit sought, Robinson’s “standard part”, without all that tedious mucking about in shrinking deltas and epsilons.
May 27, 2011 at 1:10 pm |
I recently stumbled across “dual numbers” from wikipedia and wondered if you could use it build calculus for first-year students without using limits. Polynomial derivatives, product rule, chain rule, quotient, fractional power rule all appeared quite trivial compared to the limit approach.
You could also define continuity by saying that f is continous if f(x+ydx) is inifinitesmally close to f(x) for every value of y and then show that you only need to consider y = -1 and y = +1. You can easily also show that every function with derivative is continuous but the reverse is not necessarily true. |x| is an easy counterexample.
But then I ran into trouble. How do you show that:
– every continuous function has the intermediate value property
– every continuous function on a closed and bounded interval achieves its maximum
– Rolle’s Theorem, the Mean Value Theorem
– if a function’s derivative is everywhere zero, then that function must be a constant function
– every continuous function has an anti-deritative
– how do you build Riemann Sums and integrals
– for every function with a derivative, it is increasing on an interval if and only if its derivative is greater than or equal to zero everywhere.
I ran into these problems when trying to define ln(x) by saying it is the anti-derivative of 1/x and ln(1) = 0 and then defining exp(x) as the inverse of ln(x)
December 6, 2011 at 8:07 pm |
I’m looking for more information about correspondence courses…
[…]Non-nonstandard Calculus, I « The Everything Seminar[…]…
October 4, 2012 at 11:58 pm |
\textbf{The new axiom system}
The view of the mainstream in the mathematical world from K. Weierstrass up to bevor A. Robinson to the quantities of infinity (large or small) is that they are only a process, denoted and etablished in form of limit. Infinite quantities were not allowed to exist as free, independent variables. As $ latex x\rightarrow 0$, $ latex x$ is always a variable of a function $ latex f(x)$, or as $ latex n\rightarrow\infty$, $ latex n$ must be an index of a sequence $ latex (a_n)$. Paul Du Bois-Reymond has an effort to treat infinite quantities by giving them a form of functions having the same limit of one unique variable. This approach has natural constriction and it’s acceptance by the other mathamaticians is only very limitted. We will discuss a theorem of him, which is true and according Hardy very important, but, for us, it leads us to misconception of the substance of infinity. Since Robinson, the existence of infinity quantities is assured, but in form of new numbers, the so called hyperreal numbers. The infinity quantities are now free and independent numbers, and it works very well, as it must be. But by his influence and that of Nelson, we must see the world as two parts: the standard one and the extended non-standard one. One fact is not changed at every aproach, that the infinity quantity is a problem of the conception. We will say more, infinity quantity can be used to study matters of perception.
We now introduce a new approach to the non-standard analysis and the basic concept is to introduce not new numbers to the real numbers, but a new order to the basic order $ latex <$ in the body of the real numbers.
The new order is a binary relation, called as infinity order or infinity relation, denoted as $ latex \sqsubset$. $ latex a \sqsubset b$ means $ latex a$ is infinitely small to $ latex b$. This order is definited by 6 axioms.
(U1) $ latex \sqcup(a\sqsubset b,a\sim b, a\sqsupset b)$
(U2) $ latex a\sqsubset b\wedge c\neq 0\;\rightarrow\; ac\sqsubset bc$
(U3) $ latex \sqsubset$ is arbitrarily transitive.
(U4) $ latex \sim$ is finitely transitive.
(U5) $ latex a_1,a_2\sim b\;\rightarrow \;|a_1|+|a_2|\sim b$
(U6) $ latex a\sqsubset b\;\rightarrow \;a<|b|$
Notes and explanations to the axioms:
– (U1) is the trichotomy law of the infinity like the analogous of the order $ latex <$ :
$ latex \sqcup(ab)$
I.e. it is true exactly either $ latex ab$.
The relations $ latex =,\ge,\le$ are only secondary relations of the basic relation $ latex <$. The equality = is logically definited by this trichotomy law of $ latex <$.
In this spirit we can define some secondary relations of the infinity order as follow.
$ latex a$ ist infinitely large to $ latex b$ :
$ latex a\sqsupset b:\Leftrightarrow b\sqsubset a$
$ latex a$ is equivalent or comparable with $ latex b$ :
$ latex a\sim b:\Leftrightarrow \neg(a\sqsubset b)\wedge\neg(a\sqsupset b)$
$ latex a$ is not infinitely small to $ latex b$ :
$ latex a\sqsupseteq b:\Leftrightarrow\neg (a\sqsubset b)
$ latex a$ is not infinitely large to $ latex b$ :
$ latex a\sqsubseteq b:\Leftrightarrow\neg (a\sqsupset b)$
$ latex a$ is approximate or infinitely close to $ latex b$ :
$ latex a\approx b:\Leftrightarrow a-b\sqsubset 1$
If $ latex a\approx 0$ i.e. $ latex a\sqsubset 1$, we say, $ latex a$ is infinitely small, or infinitesimal.
If $ latex a \sqsupset 1$, we say, $ latex a$ is infinitely large.
If $ latex a\sim 1$, we say, $ latex a$ is finite.
The order $ latex \sqsubset$ is not really new. In physics we now it as the relation $ latex \ll$, and on the other hand we know the notions of Landau
$ latex a\sqsubset b\leftrightarrow a=o(b),$
$ latex a\sqsubseteq b\leftrightarrow a=O(b).$
But now we introduce it as a complete \textbf{\textit{basic relation among the free real numbers}} with 6 Axioms. (Landau-notation is often defined as relation between 2 functions.)
The half-order $ latex \sqsubseteq$ is not antisymmetric. The body of the real numbers within the meaning of the standard analysis is
$ latex \mathcal{R}=(\mathbb{R},+,.,<),$
where $ latex \mathbb{R}$ is the set of the real numbers.
The body of the real numbers within the new meaning is
$ latex \mathcal{R^*}=(\mathbb{R},+,.,<,\sqsubset).$
– (U2) means, infinity order is invariant regarding the Multiplication.
– (U3) means
$ latex a_1\sqsubset a_2\sqsubset … \sqsubset a_n\quad \rightarrow\quad a_1\sqsubset a_n,$
where $ latex n$ can be arbitrarily infinite or finite.
– (U4) means
$ latex a_1\sim a_2\sim … \sim a_n\wedge n\sim 1\quad \rightarrow\quad a_1\sim a_n.$
– (U5) is equivalent with
$ latex a_1,a_2,…,a_n\sim b\wedge n\sim 1\quad \rightarrow\quad|a_1|+|a_2|+…+|a_n|\sim b$
– (U6) implies $ latex 1\sim 1$ and (U5) secures us, that $ latex 2,3,1000, 10^32,…$ are finite natural numbers.
In the next topic we show a small part of the huge arithmetics of the infinity order.
March 22, 2013 at 6:59 pm |
I am extremely impressed with your writing skills and also with the layout on your blog.
Is this a paid theme or did you modify it yourself?
Either way keep up the nice quality writing, it is rare to see a nice blog like this
one today.
March 25, 2013 at 1:37 pm |
It is really a great and helpful piece of information. I’m happy that you just shared this useful info with us. Please stay us up to date like this. Thanks for sharing.
March 26, 2013 at 5:46 pm |
Hey I am so glad I found your blog, I really found you
by mistake, while I was searching on Digg for something
else, Regardless I am here now and would just like to say kudos
for a marvelous post and a all round exciting blog (I also love the theme/design), I
don’t have time to go through it all at the moment
but I have saved it and also added your RSS feeds, so when I
have time I will be back to read a lot more, Please do keep up the fantastic jo.
April 12, 2013 at 3:16 pm |
Excellent beat ! I wish to apprentice while
you amend your site, how could i subscribe for a blog site?
The account aided me a applicable deal. I had been
a
little bit familiar of this your broadcast provided vivid
transparent concept
May 10, 2013 at 10:35 pm |
Dodatak zamišljen sugestija iskreno prognoza tako.
Me sanovnik ubistvo alge nespretno.Sanjati brojeve val zadovoljni sanjati
ujed vuka. Pijuk oblačan grudnjak ozbiljno povezati vam. Ništa sta znaci sanjati ratluk iz prkosno.
Velika hrvatska sanjarica žvakati njega sanovnik lopov.
July 10, 2013 at 5:07 pm |
Hi, I just read almost the entire blog in one weekend, and I liked it very much. I was wandering if there any way to get notes or some slide-shows of your calculus lectures?
July 26, 2013 at 1:08 pm |
Terrific work! This is the type of info that are
supposed to be shared across the net. Shame on the seek
engines for not positioning this put up upper!
Come on over and discuss with my site . Thanks =)
July 28, 2013 at 2:42 pm |
Hello to every single one, it’s really a fastidious for me to pay a visit this site, it consists of helpful Information.
August 3, 2013 at 3:29 pm |
What’s Going down i’m new to this, I stumbled upon this I have found
It absolutely useful and it has aided me out loads.
I hope to contribute & assist other customers like its helped me.
Great job.
August 4, 2013 at 12:30 pm |
Hey there! Would you mind if I share your blog with my
myspace group? There’s a lot of people that I think would really appreciate your content. Please let me know. Thank you
August 11, 2013 at 12:03 am |
Unquestionably consider that which you stated.
Your favourite justification seemed to be on the internet the simplest factor to have in mind of.
I say to you, I certainly get annoyed even as folks think about issues
that they just don’t recognize about. You managed to hit the nail upon the highest and defined out the entire thing with no need side effect , other people could take a signal. Will probably be back to get more. Thank you
August 23, 2013 at 10:24 am |
Perfect job! However this is the kind of details that are meant to be provided round the world-wide-web.
Disgrace on the seek engines for no longer placing this particular content upper!
Come on over and visit my internet site . Thank you very much =)
October 9, 2013 at 6:59 am |
I have leqrn a few good stuff here. Certainly price
bookmarking for revisiting. I surprise howw so much effort you put tto create this kind
of magnificent informative web site.
January 22, 2014 at 7:51 am |
I just like the valuable info you provide on your articles.
I’ll bookmark your blog and check again here regularly. I am
slighly certain I will be told lots of new stuff proper right here!
Beest of luck for the following!
February 13, 2014 at 9:57 am |
Fantastic beat ! I wish to apprentice whilst you
amend your website, how can i subscribe for a
blog web site? The account aided me a appropriate deal. I
have been a
little bit familiar of this your broadcast offered shiny
clear idea
September 13, 2016 at 9:48 pm |
If you are interested in topic: earn online philippines breaking new today – you should read
about Bucksflooder first
October 30, 2016 at 3:40 pm |
Democritus of Abdera knew about non-standard analysis thousands of years ago. If a cone or pyramid is mathematically cut in a horizontal plane parallel to its base, what are we to make of the surfaces it has produced? Are they equal in surface area or not? If they be unequal, then the side of a cone or pyramid is jagged like a series of steps (think of the Great Pyramid in Giza). However, if they be equal, that would imply that two adjacent intersecting planes are equal, which would mean that the cone or pyramid, being made up of equal rather than unequal circles or squares respectively, must have the same appearance as a circular cylinder or square cylinder; which is utterly absurd.
December 19, 2016 at 3:29 pm |
I devised a way to do something similar, but I only presented it in a seminar, and I did not complete the development for a few reasons: (a) Analysts seem particularly annoyed at anyone using nonstandard analysis or anything like it, and I don’t have any other logicians around here or nonstandard analysts to talk to;
(b) Most students here are Engineering students who hate Mathematics or being asked to do anything not in the textbook, and I tend to get assigned mainly service courses to teach – only recently I found myself teaching Advanced Calculus for the second time, and I used three texts. Of these three texts, one was Keisler’s Elementary Calculus text, and another was a traditional text. It worked very well, in the sense that the students seem to enjoy very much the comparison of the methods – but I was working with more advanced students who want to prove some theorems occasionally;
(c) I found out that John L. Bell (one of the authors of the textbook Models and Ultraproducts: An Introduction, which I use when teaching Mathematical Logic) wrote a textbook called A Primer of Infinitesimal Analysis, in which he develops rather fully the notion of nil-square infinitesimals for Smooth Analysis, in which the Foundations of the reasoning system are based upon Topoi Theory and all functions are analytic. I am interested in doing research, and developing a significant amount of material that re-invents the wheel is not good for that career.
Here’s the gist of what I developed along these lines and presented in seminar, before reading about nil-square analysis, and what I think about it for teaching calculus, much like the way you describe:
1. Embed the real numbers into the ring of upper triangular (2×2) matrices via the map that takes a real number r to the matrix rI, where I is the (2×2) identity matrix.
2. Restrict attention to the subring containing only the matrices of the form rI+[\vec{0} y\vec{e}_1], where \vec{e}_1 is the first column of the identity matrix, and each of r and y is a real number.
3. Denote [\vec{0} \vec{e}_1] by \varepsilon. This is our “unit infinitesimal”.
4. Order this subring using an essentially lexicographic ordering: rI+y<sI+z means that either r<s or r=s and y<z.
5. Notice that if s is a positive real number, then for every positive real number r, 0I+0\varepsilon<0I+s\varepsilon<rI+0\varepsilon, and we can interpret this as 0<s\varepsilon<r, meaning that \varepsilon and all of its positive multiples are infinitesimal, in the same sense as fluxions or Leibniz infinitesimals or nonstandard analysis, with the twist that here, actually, s\varepsilon is also algebraically nil-square, as in your definition.
6. One can then proceed as you did, to develop nil-square analysis, because we have a model with which students can compute, using the matrix algebra that they learned from their college algebra course, and the notion of "less than" is not at all a secret.
7. In this context, the monad of a number rI+s\varepsilon is the set of all numbers of the form rI+t\varepsilon, where t is any real number.
8. One loses the field properties for the ring of numbers of the form rI+s\varepsilon, but for smooth analysis, one essentially doesn't need it. The trouble is that to do non-smooth analysis well and efficiently, one needs to have inverses of non-zero infinitesimals, or at least for some of them. (At least, I haven't seen a way to overcome the need for the notion of an infinite nonstandard real number, if one is going to try to completely capture the notions of limits, including infinite limits, for calculus…)
9. One can embed the real numbers into upper triangular matrices, to obtain nil-cubed analysis, in a very similar manner, and one can define an order that provides us with different kinds of infinitesimals, so that some infinitesimals are in a sense "infinitely" smaller than others, mimicking a nice property of nonstandard analysis in which there can be infinitesimals a and b whose ratio is infinite. This is because you can include in the resulting ring of (3×3) upper triangular matrices both nil-square and nil-cubed infinitesimals, and you can build the ordering so that the nil-square infinitesimals are all larger than the nil-cubed ones. The hitch is that you must also be more careful in ordering the multiple kinds of nil-square kinds of infinitesimals. Of course, this idea can be extended to obtain nilpotent infinitesimals of all finite orders of nil-potency, none of which are invertible, and one can carefully prescribe the ordering on the resulting ring, so as to have infinitely many kinds of size relationships between the different kinds of infinitesimals that mimic the "infinite ratio" property I mentioned above for nonstandard infinitesimals a la Robinson.
10. You can do the same kind of thing with infinite upper triangular matrices, and the direct sum, or the direct limit, of the spaces described above should be a natural way to think of a restricted version of this. I've not worked on any of the details, but if you consider only those infinite matrices that are upper triangular with only a finite number of off-diagonal nonzero entries, and that are constant on the diagonal, then this extension ring of the ring of real numbers will include infinitely many kinds of nil-potent infinitesimals of every order of nil-potency, and you should be able to order it "lexicographically" so that a plethora of "ratios" of infinitesimals is obtained.
11. The "courses" described in 9 and 10 are too advanced for freshman calculus students, but the earlier material could be reasonably developed for reasonably talented freshman students…
12. If you don't restrict the ring of infinite matrices to those with only finitely many nonzero off-diagonal entries, then you have available non-nilpotent infinitesimals, ordered in a natural way to extend the ordering of the reals that are embedded in that ring as I described above. They still are not invertible, however.
13. I mentioned this idea to my adviser, who had introduced me to nonstandard analysis as a graduate student. He said it sounds like Lie Algebras and Lie Groups. That's when I stopped thinking I had done something "new", because I realized that the theory of Lie Algebras and Lie Groups provides a lot of concrete models for this kind of abstraction, even if the Lie Theory is not accessible to most freshmen.
December 19, 2016 at 3:36 pm |
I cannot edit my previous comment, so as to notify me via email if anyone comments (I had some technical difficulties when I first tried to post my comment, and when I posted it again, I realized too late that I forgot to click the “Notify me…” link), so please reply here, so I will be notified.
I also did not realize that I was going to be billed as “Anonymous”.
January 18, 2017 at 1:54 am |
Vamos a ver, Jose: Lo de la luna cóncava no hay que pensar mucho ni ser un científico para saber que tiene más inclinación que una luna tradicional (en el C6), por lo que las gotas de agua salen más rápidamente. Imgínate por un momento Alvaro que en estos momentos de crisis en España te pasees con un Mercedes último modelo de 50.000 euros por algún lugar de la España. Ayer hice viaje a Madrid desde Burgos y a la vuelta tuve la oportunidad de tropezarme con un C6 color plata.
December 12, 2017 at 12:10 pm |
Normally I don’t learn post on blogs, but I would like to say that this write-up very pressured me to check out and do so! Your writing taste has been amazed me. Thank you, very great article.
May 24, 2019 at 12:14 am |
cornellmath.wordpress.com is good, solid content. I just passed this on 5/24/2019 to a coworker who’s been doing some work of their own on this subject. To say thanks, he just bought me a drink! So, let me express my gratitude by saying: Thanks for the drink!
August 16, 2020 at 9:03 am |
Another approach to teaching calculus without limits is by using hyperreal numbers, which I believe to be much more logical than dual numbers. Hyperreal numbers allow for differentials to be manipulated algebraically, even in higher-order derivatives. This turns calculus into just a regular extension to algebra, which students readily understand. My approach is given in the book “Calculus from the Ground Up”. You can get an overview in the paper “Simplifying and Refactoring Introductory Calculus”.